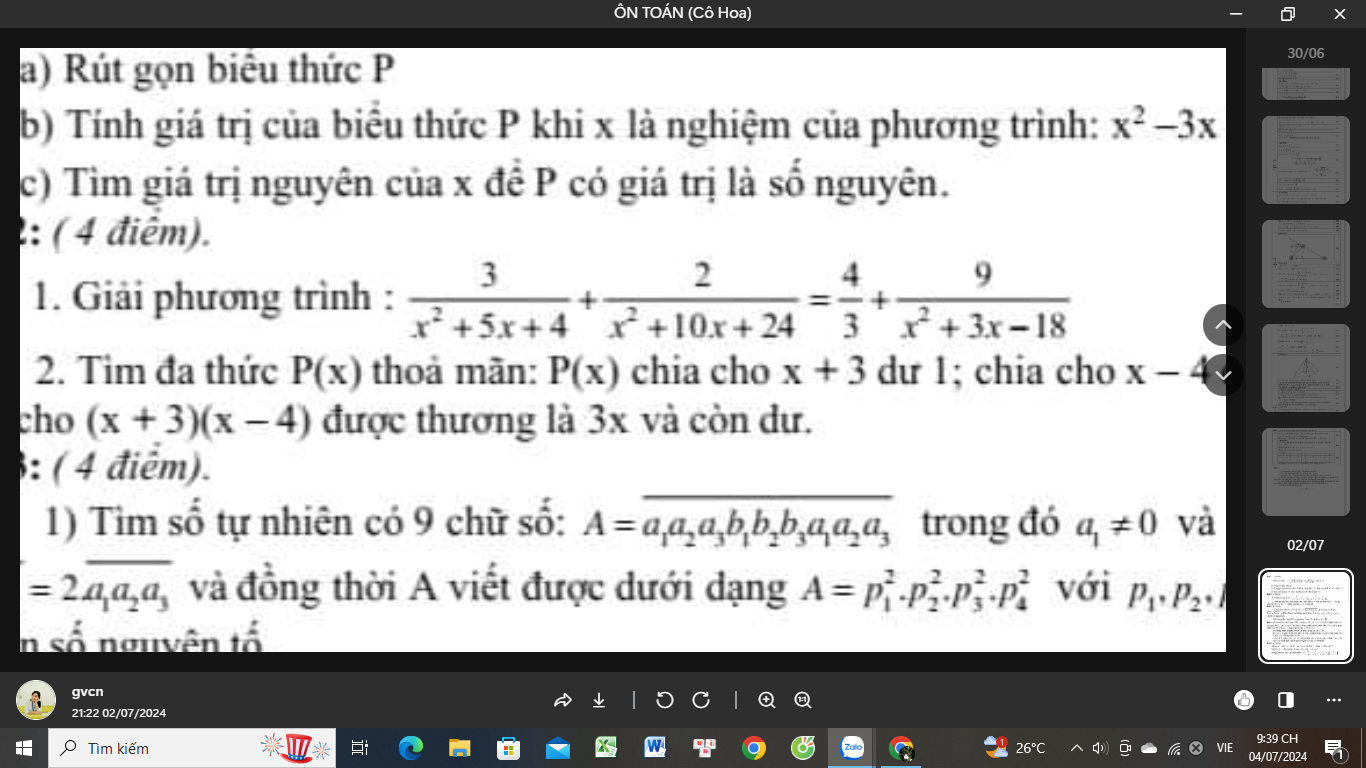
giúp mình câu giải phương trình với nhé , tốt giải hết cũng đc ạ :))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
1
Những câu hỏi liên quan
NN
1 tháng 11 2020
\(A=x^4-6x^3+ax^2+bx+1\)
Để A là bình phương của 1 đa thức thì \(A=\left(x^2+cx+1\right)^2\)
\(\Rightarrow A=x^4+c^2x^2+1+2cx^3+2x^2+2cx\)
\(=x^4+2cx^3+\left(2+c^2\right)x^2+2cx+1\)
Đồng nhất hệ số ta có: \(\hept{\begin{cases}2c=-6\\2+c^2=a\\2c=b\end{cases}}\Leftrightarrow\hept{\begin{cases}c=-3\\2+\left(-3\right)^2=a\\2.\left(-3\right)=b\end{cases}}\Leftrightarrow\hept{\begin{cases}c=-3\\a=2+9\\b=-6\end{cases}}\Leftrightarrow\hept{\begin{cases}c=-3\\a=11\\b=-6\end{cases}}\)
Vậy \(a=11\)và \(b=-6\)
16 tháng 11 2021
#include <bits/stdc++.h>
using namespace std;
int a,b,x;
int main()
{
cout<<"Nhap a: ";
cin>>a;
cout<<"Nhap b: ";
cin>>b;
if(a==0)
{
if(b==0)
{
cout<<"Phuong trinh vo so nghiem"<<endl;
}
else
{
cout<<"Phuong trinh vo nghiem"<<endl;
}
}
else
{
x=-b/a;
cout<<"Phuong trinh co nghiem la: "<<x<<endl;
}
Return 0;
}
3 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2
Đa thức biểu thị kết quả thứ hai: H = (x – 1)2
Đa thức biểu thị kết quả cuối cùng:
Q = K – H = (x + 1)2 - (x – 1)2
= (x+1).(x+1) - (x – 1). (x – 1)
= x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1)
= x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)]
= x2 + x + x + 1 – (x2 – x – x + 1)
= x2 + x + x + 1 – x2 + x + x – 1
= (x2 - x2 ) + (x+x+x+x) + (1- 1)
= 4x
Để tìm x, ta lấy kết quả cuối cùng chia cho 4
MT
6 tháng 3 2020
a) Ta có \(P\left(x\right)=\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)+a\)
\(=\left(x+1\right)\left(x+7\right)\left(x+3\right)\left(x+5\right)+a\)
\(=\left(x^2+8x+7\right)\left(x^2+8x+15\right)+a\)
Đặt \(b=x^2+8x+9\) khi đó P(x) có dạng:
\(\left(b-2\right)\left(b+6\right)+a=b^2+4b+a-12=b\left(b+4\right)+a-12\)
nên để \(P\left(x\right)⋮Q\left(x\right)\Leftrightarrow a-12=0\Leftrightarrow a=12\)
12 tháng 4 2017
Chỉ ra 1 nghiệm của đa thức đúng không
Giả sử d là 1 nghiệm của đa thức thì:
\(\Rightarrow\)f(x) = (x - d)(x2 + mx + n)
= x3 + (m - d)x2 + (n - dm)x - dn = x3+ax2+bx+c
Đồng nhất thức 2 vế ta được
m - d = a; n - dm = b; -dn = c
Thế vào điều kiện đề bài ta được
m - d + 2(n - dm) - 4dn = - 0,5
\(\Leftrightarrow\)2d( 4n + 2m + 1) = (4n + 2m + 1)
\(\Leftrightarrow\)(4n + 2m + 1)(2d - 1) = 0
(Ta không cần quan tâm đến (4n + 2m + 1) vì mục đích ta tìm d thôi)
\(\Rightarrow2d-1=0\)
\(\Leftrightarrow d=\frac{1}{2}\)
Vậy đa thức có 1 nghiệm là \(\frac{1}{2}\)
ĐKXĐ: \(x\notin\left\{-1;-4;-6;3\right\}\)
\(\dfrac{3}{x^2+5x+4}+\dfrac{2}{x^2+10x+24}=\dfrac{4}{3}+\dfrac{9}{x^2+3x-18}\\ \Leftrightarrow\dfrac{3}{\left(x+1\right)\left(x+4\right)}+\dfrac{2}{\left(x+4\right)\left(x+6\right)}-\dfrac{9}{\left(x-3\right)\left(x+6\right)}=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+6}-\left(\dfrac{1}{x-3}-\dfrac{1}{x+6}\right)=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x-3}=\dfrac{4}{3}\\ \Leftrightarrow\dfrac{x-3-x-1}{\left(x+1\right)\left(x-3\right)}=\dfrac{4}{3}\\ \Rightarrow4\left(x^2-2x-3\right)=3.\left(-4\right)\\ \Leftrightarrow4x^2-8x-12=-12\\ \Leftrightarrow4x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=2\left(tm\right)\end{matrix}\right.\)