ai học giỏi phương trình ng nguyên kb với mình, ad cho em đăng post này, e cám cơn ad nhìu ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2022
\(\Leftrightarrow\left\{{}\begin{matrix}8x-20y=44\\15x+20y=25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
T
1
22 tháng 4 2023
cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm
NA
28 tháng 2
Bước 1: Xét tam giác vuông \(A C E\)
Vì \(C E \bot A B\), ta có \(\triangle A C E\) vuông tại \(E\). Theo định lý Pythagoras:
\(A C^{2} = A E^{2} + E C^{2}\)
Bước 2: Xét tam giác vuông \(A C F\)
Tương tự, vì \(C F \bot A D\), ta có \(\triangle A C F\) vuông tại \(F\), nên:
\(A C^{2} = A F^{2} + C F^{2}\)
Bước 3: Xét tổng hai phương trình
Từ hai phương trình trên:
\(A E^{2} + E C^{2} + A F^{2} + C F^{2} = 2 A C^{2}\)
Mặt khác, trong hình bình hành, ta có tính chất:
\(E C^{2} = A F \cdot A D , C F^{2} = A E \cdot A B\)
Thay vào phương trình:
\(A E^{2} + A F^{2} + A E \cdot A B + A F \cdot A D = 2 A C^{2}\)
Do hình bình hành có tính chất đối xứng, ta cũng có:
\(A E^{2} + A F^{2} = A C^{2}\)
Suy ra:
\(A C^{2} + A E \cdot A B + A F \cdot A D = 2 A C^{2}\)
Từ đó suy ra:
\(A E \cdot A B + A F \cdot A D = A C^{2}\)
20 tháng 2 2020
a) Ta có tam giác ABC cân tại A nên: \(\widehat{B}=\widehat{C}=\frac{180^0-\widehat{A}}{2}\)(1)
Xét tam giác ADE có AD=AE (gt)
=> tam giác ADE cân tại A => \(\widehat{AED}=\widehat{ADE}=\frac{180^0-\widehat{A}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AED}=\widehat{B}\)
Mà 2 góc ở vị trí đồng vị nên \(DE//BC\)(đccm)
b)Ta có AB=AE+EB và AC=AD+CD mà AB=AC, AE=AD => EB= CD
Xét tam giác BEC, tam giác BCD có:
EB= CD
\(\widehat{B}=\widehat{C}\)
BC chung
=> tam giác BEC= tam giác CDB ( c_g_c)
=>\(\widehat{BEC}=\widehat{BDC}=90^0\)
=> \(CE\perp AB\)(ĐCCM)
CH
Cô Hoàng Huyền
Admin
VIP
5 tháng 1 2018
Câu hỏi của bggvf - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo bài tương tự tại link trên nhé.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
5 tháng 6 2023
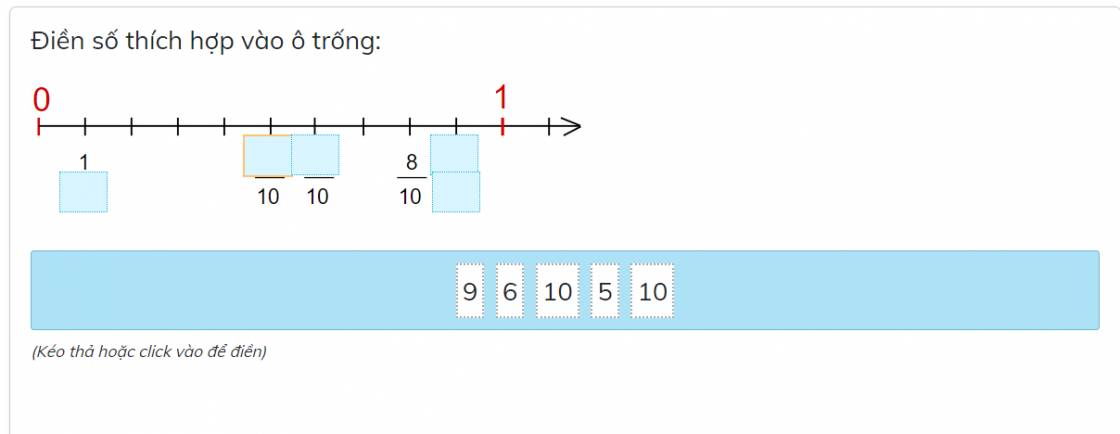
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
5 tháng 6 2023
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!