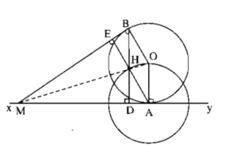
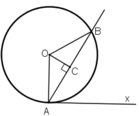
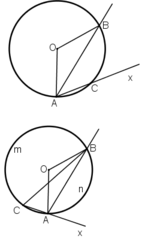
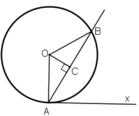
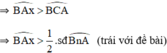Cho đường thẳng d cố định ở ngoài đường tròn (O;R). Khoảng cách từ O đến d không nhỏ hơn R√2𝑅2. Từ 1 điểm M thuộc d dựng các tiếp tuyến MA, MB đến đường tròn tâm O (A, B là các tiếp điểm). Dựng cát tuyến MCD( tia MC nằm giữa hai tia MO, MA và MC<MD). Gọi E là trung điểm của CD. H là giao điểm của AB và MO
CM:
a) Các tiếp tuyến tại C và D của đường tròn (O) cắt nhau tại 1 điểm nằm trên đường thẳng AB
b) Đường thẳng AB luôn đi qua 1 điểm cố định

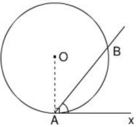
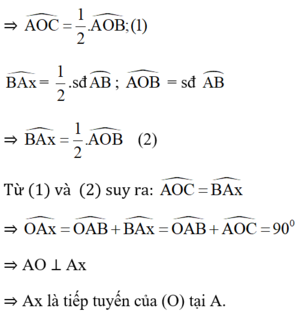

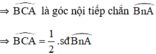
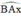 là góc ngoài của tam giác BAC
là góc ngoài của tam giác BAC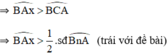
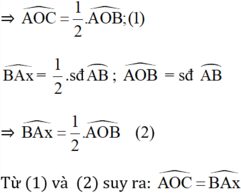
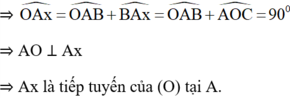
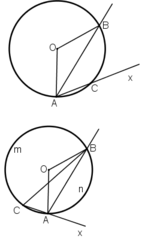

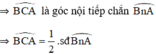
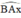 là góc ngoài của tam giác BAC
là góc ngoài của tam giác BAC