Cho hàm số f(x) = ax2 + bx + c (a, b, c . Biết f(-1) ⋮ 3; f(0) ⋮ 3; f(1) ⋮ 3. Chứng minh rằng a, b, c đều chia hết cho 3.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2019
Ta có f x = 4 x 2 + 4 x + 3 2 x + 1 dx
= ∫ 2 x + 1 + 2 2 x + 1 d x = x 2 + x + ln x + 1 + C
Do f(0) = 1 nên c = 1. Suy ra f x = x 2 + x + ln 2 x + 1 + 1
Vậy a : b : c = 1 : 1 : 1
Đáp án B
PV
17 tháng 2 2024
Sao ra được chỗ dấu = thứ 2. 5ax^+(3b-6a)x+c-3b/√2x-3 á, thắc mắc
UN
0
UN
0
CM
24 tháng 5 2017
Ta có:
f(x+3) = a(x+3)2+ b(x+3) +c=ax2+ (6a+b) x+ 9a+ 3b+c
f(x+2) = a(x+2)2+ b(x+2) +c=ax2+ (4a+b) x+ 4a+ 2b+c
f (x+1) = a(x+1)2+ b(x+1) +c=ax2+ (2a+b) x+ 2a+ 2b+c
Suy ra: (x+ 3) -3f( x+ 2) +3f( x+ 1)= ax2+ bx+ c
Chọn D.
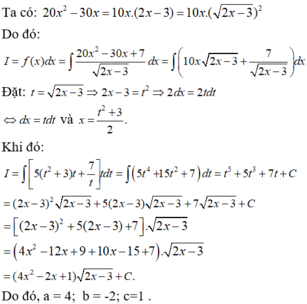
\(f\left(-1\right)=a\cdot\left(-1\right)^2+b\cdot\left(-1\right)+c=a-b+c\) ⋮ 3
\(f\left(0\right)=a\cdot0^2+b\cdot0+c=c\) ⋮ 3
\(f\left(1\right)=a\cdot1^2+b\cdot1+c=a+b+c\) ⋮ 3
Ta có: `a-b+c⋮3` và `a+b+c⋮3`
=> `a-b+c+a+b+c` ⋮ 3
=> `2a+2c` ⋮ 3
Mà: c ⋮ 3 => 2c ⋮ 3
=> `2a` ⋮ 3
=> `a⋮3`
a + b + c ⋮ 3
Trong đó có a ⋮ 3 và c ⋮ 3
=> b ⋮ 3