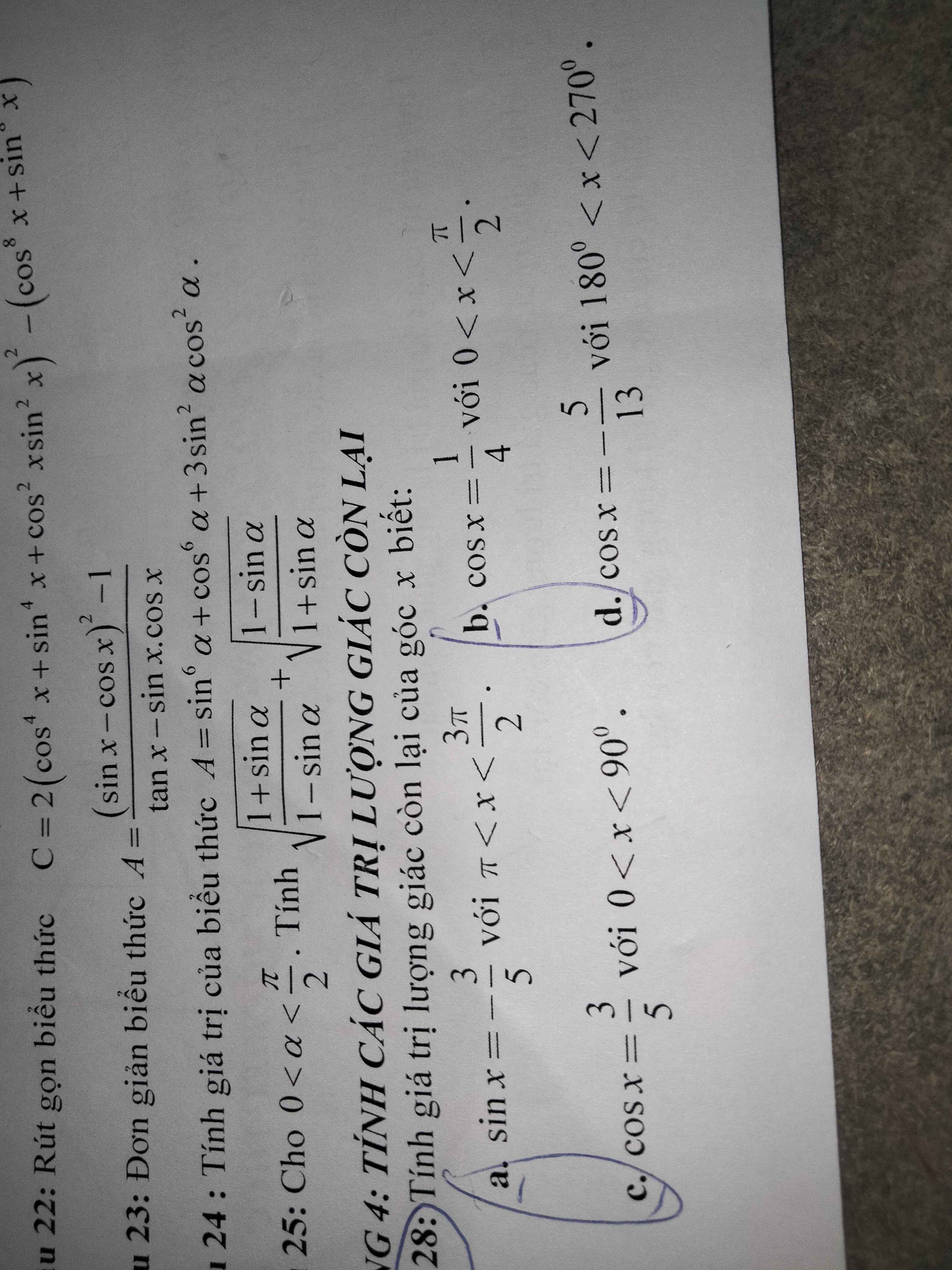
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Sửa đề: C/m tứ giác BEHC nội tiếp
Xét tứ giác BEHC có
\(\widehat{BEC}=\widehat{BHC}\left(=90^0\right)\)
\(\widehat{BEC}\) và \(\widehat{BHC}\) là hai góc cùng nhìn cạnh BC
Do đó: BEHC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

Phép nhân hoá:
Ví dụ: Bác gấu đang bảo vệ những chú hươu khỏi đàn sói hung ác

- Bước sang thế kỉ XVI, triều đình nhà Lê càng suy yếu thì sự tranh chấp giữa các phe phái phong kiến càng diễn ra quyết liệt.
- Mạc Đăng Dung vốn là một võ quan. Lợi dụng xung đột giữa các phe phái, đã tiêu diệt các thế lực đối lập, thâu tóm mọi quyền hành, cương vị như Tể tướng.
- Năm 1527, Mạc Đăng Dung cướp ngôi nhà Lê, lập ra triều Mạc (Bắc triều).
- Năm 1533, một võ quan triều Lê là Nguyễn Kim chạy vào Thanh Hoá, lập một người thuộc dòng dõi nhà Lê lên làm vua, lấy danh nghĩa "phù Lê diệt Mạc", sử cũ gọi là Nam triều để phân biệt với Bắc triều (nhà Mạc ở phía bắc).
=> Cục diện Nam - Bắc triều hình thành.
Bước sang thế kỉ XVI, triều đình nhà Lê càng suy yếu thì sự tranh chấp giữa các phe phái phong kiến càng diễn ra quyết liệt. Mạc Đăng Dung vốn là một võ quan. Lợi dụng xung đột giữa các phe phái, đã tiêu diệt các thế lực đối lập, thâu tóm mọi quyền hành, cương vị như Tể tướng. Năm 1527, Mạc Đăng Dung cướp ngôi nhà Lê, lập ra triều Mạc (Bắc triều). Năm 1533, một võ quan triều Lê là Nguyễn Kim chạy vào Thanh Hoá, lập một người thuộc dòng dõi nhà Lê lên làm vua, lấy danh nghĩa "phù Lê diệt Mạc", sử cũ gọi là Nam triều để phân biệt với Bắc triều (nhà Mạc ở phía bắc).


2 They live in a small town which has 500 inhabitants
3 The police haven't found the robber who stole $50000
4 I lend her "Hamlet", which is really interesting to read
5 I don't remember he name of the man whom I met at the bus stop
6 Tom told me about the job which he sastifed
1. Oleg has an iron box and he kept his letters in the box
2. They live in a small town which has 500 inhabitants
3. The police haven't found the robber who stole $50000
4. I lend her "Hamlet", which is really interesting to read
5. I don't remember he name of the man whom I met at the bus stop
6. Tom told me about the job which he sastifed

\(11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
\(S=\left\{1,\dfrac{4}{11}\right\}\)
Đặt C(x)=0
\(\Leftrightarrow11x^2-15x+4=0\)
\(\Leftrightarrow11x^2-11x-4x+4=0\)
\(\Leftrightarrow11x\left(x-1\right)-4\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(11x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\11x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\11x=4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{4}{11}\end{matrix}\right.\)
Vậy: Nghiệm của đa thức \(C\left(x\right)=11x^2-15x+4\) là 1 và \(\dfrac{4}{11}\)


a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)