Khảo sát và vẽ đồ thị hàm số $y=\dfrac{x^2-x-1}{x-2}$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

DT
31 tháng 1 2022
Tập xác định : R
Chiều biến thiên : hàm số đồng biến trên \(\left(-\infty;0\right)\)
hàm số nghịch biến trên \(\left(0;+\infty\right)\)
Lập bảng giá trị để vẽ đồ thị
HM
0

BC
2

TL
Trịnh Long
CTVVIP
4 tháng 2 2022
- Tập xác định : D = R
- Hàm số trên là hàm nghịch biến khi x > 0 và đồng biến khi x < 0
Bảng giá trị :
x -4 -2 0 2 4
y -8 -2 0 -2 -8
PV
0


CM
5 tháng 3 2018
Với m = 2 ta có hàm số 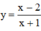
- Tập xác định : D = R\{-1}.
- Sự biến thiên :
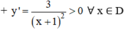
⇒ Hàm số đồng biến trên (-∞ ; -1) và (-1 ; +∞).
+ Cực trị : hàm số không có cực trị
+ Tiệm cận :

⇒ y = 1 là tiệm cận ngang của đồ thị hàm số
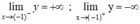
⇒ x = -1 là tiệm cận ngang của đồ thị hàm số.
+ Bảng biến thiên :
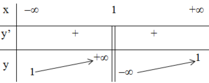
- Đồ thị :
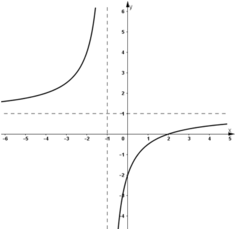

Tập xác định \(D=ℝ\backslash\left\{2\right\}\)
TCĐ: \(x=2\)
Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)
nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)
Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
BBT