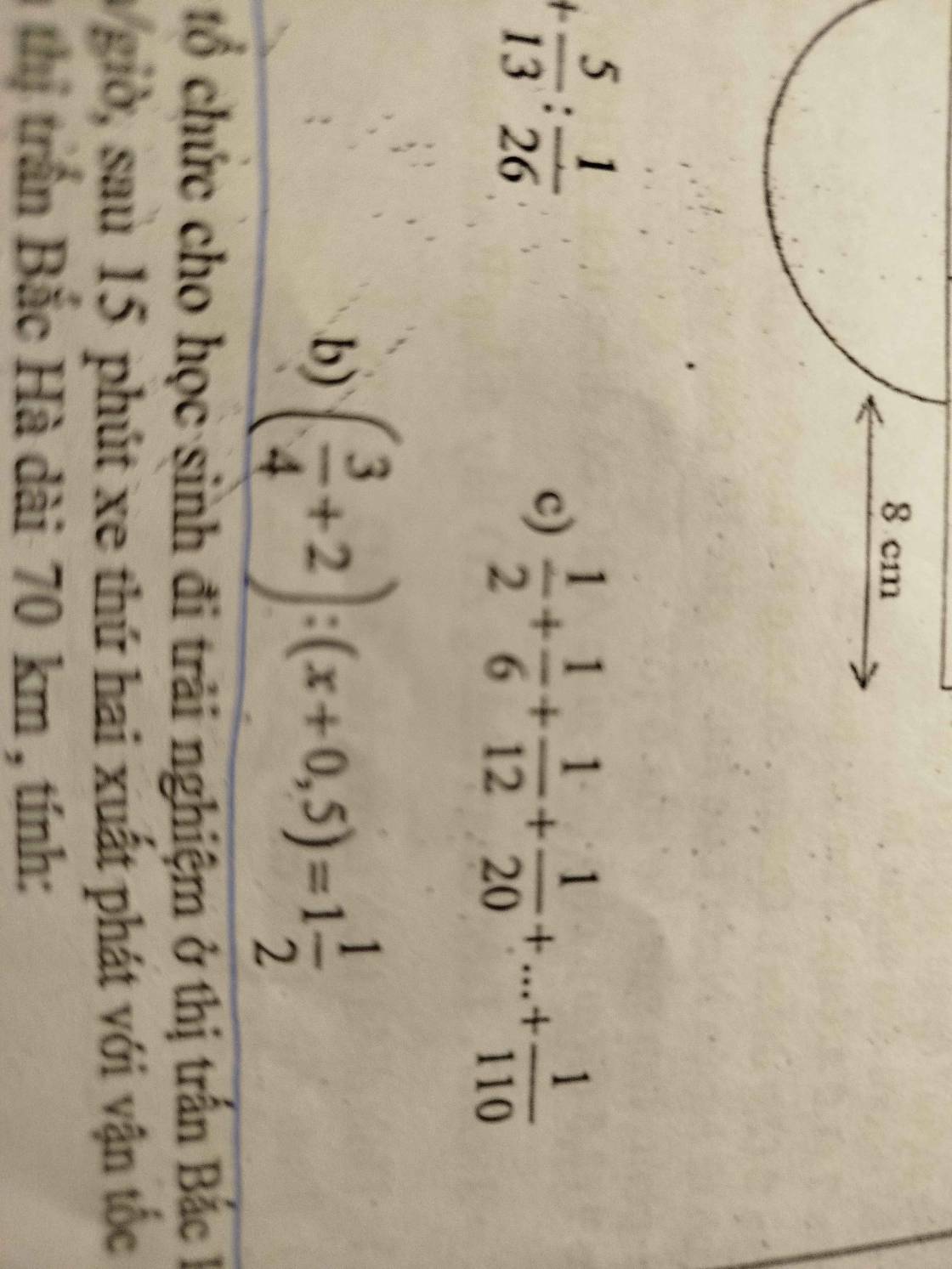 ai làm giúp mình câu tìm x này với câu b ý
ai làm giúp mình câu tìm x này với câu b ý
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) -x+8= 17
-x = 17-8
-x = 9
x = -9
b) \(\left|x+3\right|=15\)
\(\Rightarrow\orbr{\begin{cases}x+3=15\\x+3=-15\end{cases}}\Rightarrow\orbr{\begin{cases}x=12\\x=-18\end{cases}}\)
\(\Rightarrow x\in\left\{-18;12\right\}\)
c) \(\left|x-7\right|+13=25\)
\(\left|x-7\right|=12\)
\(\Rightarrow\orbr{\begin{cases}x-7=12\\x-7=-12\end{cases}\Rightarrow\orbr{\begin{cases}x=19\\x=-5\end{cases}}}\)
\(\Rightarrow x\in\left\{-5;19\right\}\)
_Học tốt nha_

a . bcd . abc = abcabc
(a . bcd) . abc = abc . 1001
a . bcd = 1001
Phân tích 1001 thành tích các thừa số nguyên tố: 1001 = 7 . 11 . 13
Suy ra a = 7; bcd = 11 . 13 = 143
Vậy a = 7; b = 1; c = 4; d = 3
a x bcd x abc = abcabc
a x bcd x abc = abc x 1001
⇒ a x bcd = 1001
⇒ a = 7 và bcd = 143

\(2x-3=\frac{x+1}{2}\)
\(\Rightarrow2\left(2x-3\right)=x+1\)
\(\Rightarrow4x-6=x+1\)
\(\Rightarrow3x=7\)
\(\Rightarrow x=\frac{7}{3}\)

\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

để B thuộc Z
=> căn x - 15 chia hết 3
căn x - 15 thuộc B(3)
=> căn x - 15 = 3K (K thuộc Z)
căn x = 3K + 15
x = (3K + 15)2
\(\frac{\sqrt{x}-15}{3}\)=\(\frac{\sqrt{x}}{3}\)-\(\frac{15}{3}\)=\(\frac{\sqrt{x}}{3}\)- 5
vì B thuộc Z => \(\frac{\sqrt{x}}{3}\)- 5 thuộc Z
=> \(\frac{\sqrt{x}}{3}\)thuộc Z
=>\(\sqrt{x}\)chia hết cho 3
=> \(\sqrt{x}\)= 9

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)

ĐKXĐ: \(x\ge\dfrac{2}{3}\)
\(\Leftrightarrow x\sqrt{3x-2}-x^2+\left(x+1\right)\sqrt{5x-1}-\left(x+1\right)^2+x^2+\left(x+1\right)^2-8x+3=0\)
\(\Leftrightarrow x\left(\sqrt{3x-2}-x\right)+\left(x+1\right)\left(\sqrt{5x-1}-x-1\right)+2\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\dfrac{-x\left(x^2-3x+2\right)}{\sqrt{3x-2}+x}+\dfrac{-\left(x+1\right)\left(x^2-3x+2\right)}{\sqrt{5x-1}+x+1}+2\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)+\left(2-\dfrac{x}{\sqrt{3x-2}+x}-\dfrac{x+1}{\sqrt{5x-1}+x+1}\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(\dfrac{\sqrt{3x-2}}{\sqrt{3x-2}+x}+\dfrac{\sqrt{5x-1}}{\sqrt{5x-1}+x+1}\right)=0\)
\(\Leftrightarrow x^2-3x+2=0\) (ngoặc đằng sau luôn dương)
\(\Leftrightarrow...\)



 ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ
ai giúp mình làm đống này với chỉ cần trả lời câu mấy ý mấy là được rồi ạ  Ai làm giúp mình câu này với ạ
Ai làm giúp mình câu này với ạ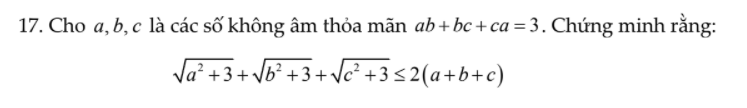 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.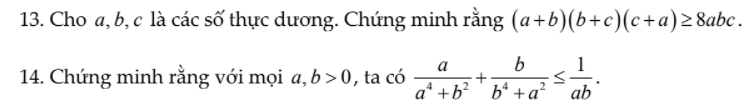

\(\left(\dfrac{3}{4}+2\right):\left(x+0,5\right)=1\dfrac{1}{2}\)
=>\(\dfrac{11}{4}:\left(x+0,5\right)=\dfrac{3}{2}\)
=>\(x+0,5=\dfrac{11}{4}:\dfrac{3}{2}=\dfrac{11}{4}\times\dfrac{2}{3}=\dfrac{11}{6}\)
=>\(x=\dfrac{11}{6}-0,5=\dfrac{11}{6}-\dfrac{3}{6}=\dfrac{8}{6}=\dfrac{4}{3}\)