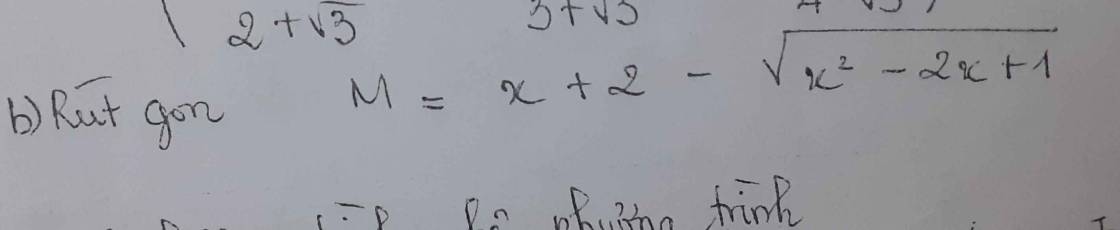 giúp e với ạ
giúp e với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)




Chiều rộng là :18:3=6(cm)
Chu vi HCN là: (18+6)×2=48(cm)
Diện tích HCN là:18×6=108(cm2)
Đ/S:48cm
108cm2
Làm theo cách này 😆😆
Chiều rộng là : 18.1/3=6(cm)
Chu vi là : (18+6).2=48(cm)
Diện tích là : 18.6=108(cm2)
Đ/S: chu vi : 48 cm
diện tích : 108 cm2
(chú ý : dấu "." là dấu nhân nha em ) Học tốt nha



Ex4
1 put
2 get up
3 sit down
4 write
5 give up
6 try on
7 tidied up
8 woke
9 fall down
10 switched on
Ex5
1 look for
2 Fill in
3 turn down
4 get on
5 Turn off
6 switch on
7 throw
8 take off
9 look

a.
Đặt \(x+2y+1=a\)
\(\Rightarrow P=a^2+\left(a+4\right)^2=2a^2+8a+16=2\left(a+2\right)^2+8\ge8\)
\(P_{min}=8\) khi \(a=-2\) hay \(x+2y+3=0\)
b.
\(\sqrt{x}-1=a\ge0\Rightarrow\sqrt{x}=a+1\Rightarrow x=a^2+2a+1\)
\(Q=\dfrac{\left(a^2+2a+1\right)+\left(a+1\right)+1}{a}=\dfrac{a^2+3a+3}{a}=a+\dfrac{3}{a}+3\ge2\sqrt{\dfrac{3a}{a}}+3=3+2\sqrt{3}\)
\(Q_{min}=3+2\sqrt{3}\) khi \(a=\sqrt{3}\) hay \(x=4+2\sqrt{3}\)





M = x + 2 - √(x² - 2x + 1)
= x + 2 - √(x - 1)²
= x + 2 - |x - 1| (1)
Với x ≥ 1, ta có:
(1) = x + 2 - x + 1
= 3
Với x < 1, ta có:
M = x + 2 - 1 + x
= 2x + 1