 giải giúp mình bài 2
giải giúp mình bài 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


35+98
=(35-2)+(98+2)
=33+100
=133
46+29
=(46+4)+(29-4)
=50+25
=75

1:
a: =12/10-7/10=5/10=1/2
b: \(=\dfrac{4}{13}-\dfrac{4}{13}+\dfrac{-5}{11}-\dfrac{6}{11}=-\dfrac{11}{11}=-1\)
2:
a: x+2/7=-11/7
=>x=-11/7-2/7=-13/7
b: (x+3)/4=-7/2
=>x+3=-14
=>x=-17


1.
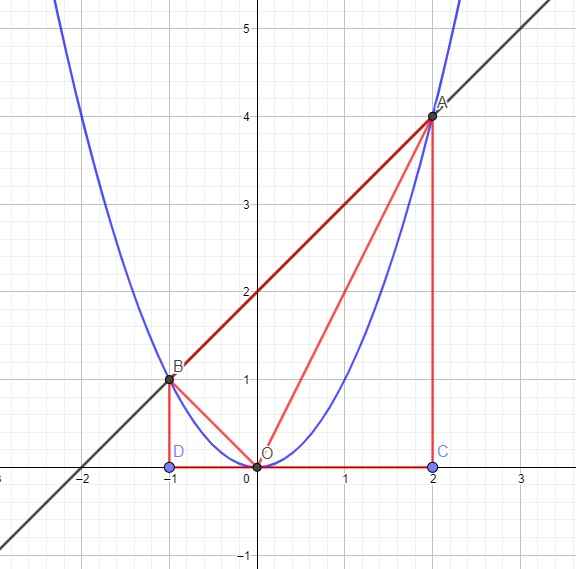
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)

Câu 2: b. \(\sqrt{9x^2-6x+1}=9\)
<=> \(\sqrt{\left(3x-1\right)^2}=9\)
<=> 3x - 1 = 9
<=> 3x = 10
<=> x = \(\dfrac{10}{3}\)

\(1,=x^3-2x^2-5x^2+10x+x-2-x^3-11x=-3x^2-2\\ 2,đề.thiếu\)

Bạn ơi, làm như vậy thì quá ngắn rồi ạ, với lại bạn làm thiếu mất đề bài của mình rồi



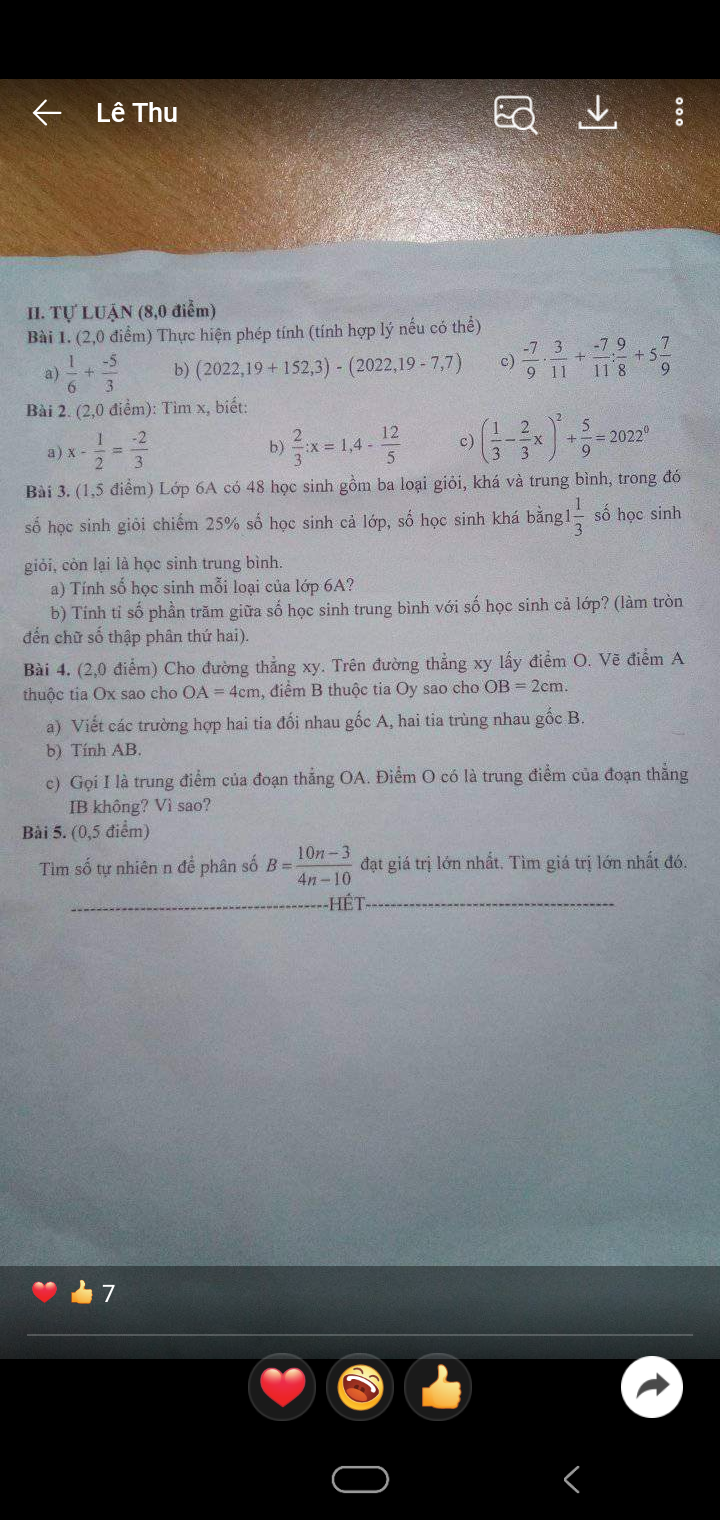

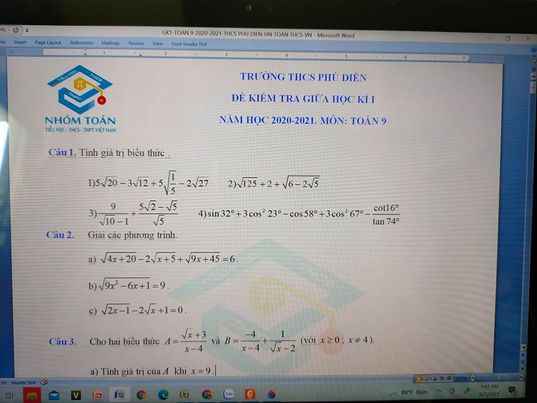 Giải giúp mình bài 1 bài 2 đi mn
Giải giúp mình bài 1 bài 2 đi mn



Bài 2:
1:
a: Thay m=2 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}3x+y=2-1=1\\x-2y=5\cdot2+2=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+2y=2\\x-2y=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7x=14\\x-2y=12\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\2y=x-12=2-12=-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=-5\end{matrix}\right.\)
b: Vì \(\dfrac{3}{1}\ne\dfrac{1}{-2}\)
nên hệ luôn có nghiệm duy nhất
\(\left\{{}\begin{matrix}3x+y=m-1\\x-2y=5m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+2y=2m-2\\x-2y=5m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}6x+2y+x-2y=2m-2+5m+2\\x-2y=5m+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7x=7m\\2y=x-5m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=m\\2y=m-5m-2=-4m-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=m\\y=-2m-1\end{matrix}\right.\)
\(T=x^2+y+12\)
\(=m^2-2m-1+12\)
\(=m^2-2m+11=\left(m-1\right)^2+10>=10\forall m\)
Dấu '=' xảy ra khi m-1=0
=>m=1
2:
a: Thay m=2 vào phương trình, ta được:
\(x^2-2\left(2+2\right)x+2^2+7=0\)
=>\(x^2-8x+11=0\)
=>\(\left(x-4\right)^2=5\)
=>\(x-4=\pm\sqrt{5}\)
=>\(x=4\pm\sqrt{5}\)
b: \(\Delta=\left(-2m-4\right)^2-4\left(m^2+7\right)\)
\(=4m^2+16m+16-4m^2-28=16m-12\)
Để phương trình có hai nghiệm phân biệt thì 16m-12>0
=>16m>12
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m+2\right)=2m+4\\x_1x_2=\dfrac{c}{a}=m^2+7\end{matrix}\right.\)
\(x_1^2+x_2^2=x_1x_2+12\)
=>\(\left(x_1+x_2\right)^2-3x_1x_2=12\)
=>\(\left(2m+4\right)^2-3\left(m^2+7\right)-12=0\)
=>\(4m^2+16m+16-3m^2-21-12=0\)
=>\(m^2+16m-17=0\)
=>(m+17)(m-1)=0
=>\(\left[{}\begin{matrix}m=-17\left(loại\right)\\m=1\left(nhận\right)\end{matrix}\right.\)