cho a b c là độ dài 3 cạnh tam giác p là nửa chu vi ab/(p-c) + bc/(p-a) + ca/(p-b)>=4p
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VP
0
TH
5 tháng 3 2020
Vì a, b, c là độ dài của 3 cạnh tam giác \(\Rightarrow a,b,c>0\)
Do chu vi của tam giác bằng 1 \(\Rightarrow a+b+c=1\Rightarrow b+c=1-a\)
Giả sử : \(ab+ac+bc>a\cdot b\cdot c\)
\(\Rightarrow ab+ac+bc-abc>0\)
\(\Rightarrow a\left(b+c\right)+bc\left(1-a\right)>0\Rightarrow a\left(b+c\right)+bc\left(b+c\right)>0\)
\(\Rightarrow\left(b+c\right)\left(a+bc\right)>0\)( thỏa mãn vì \(a,b,c>0\))
Vậy \(ab+bc+ac>a\cdot b\cdot c\)( ĐPCM )
CM
4 tháng 10 2018
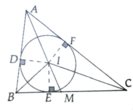
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b
30 tháng 8 2017
Do a,b,c là 3 cạnh tam giác nên \(a+b-c>0;b+c-a>0;c+a-b>0\)
Đặt \(x=b+c-a>0\)
\(y=a+c-b>0\)
\(z=a+b-c>0\)
\(\Rightarrow a=\frac{"y+z"}{2}\)
\(\Rightarrow b=\frac{"x+z"}{2}\)
\(\Rightarrow c=\frac{"x+y"}{2}\)
\(A=\frac{a}{"b+c-a"}+\frac{b}{"a+c-b"}+\frac{c}{"a+b-c"}\)
\(=\frac{"y+z"}{"2x"}+\frac{"x+z"}{"2y"}+\frac{"x+y"}{"2z"}\)
\(=\frac{1}{2}."\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\)
Áp dụng công thức bdt Cauchy cho 2 số :
\(\frac{x}{y}+\frac{y}{x}\ge2\)
\(\frac{x}{z}+\frac{z}{x}\ge2\)
\(\frac{y}{z}+\frac{z}{y}\ge2\)
Cộng 3 bdt trên, suy ra :
\("\frac{x}{y}+\frac{y}{x}+\frac{x}{z}+\frac{z}{x}+\frac{y}{z}+\frac{z}{y}"\ge6\)
\(\Rightarrow A\ge\frac{1}{2}.6=3\) "dpcm"
P/s: Nhớ thay thế dấu ngoặc kép thành dấu ngoặc đơn nhé
9 tháng 5 2021
a. Tổng BC và CA là:
12 + 7= 19(cm)
b. Chu vi tam giác ABC là:
12 + 19= 31(cm)
Đ/s: a: 19cm
b:31cm
NL
0
Đặt \(S=\frac{ab}{p-c}+\frac{bc}{p-a}+\frac{ca}{p-b}\)
Bất đẳng thức cần chứng minh tương đương với \(S=\frac{2ab}{a+b-c}+\frac{2bc}{b+c-a}+\frac{2ca}{c+a-b}\ge2\left(a+b+c\right)\)
Đặt \(a+b-c=x;b+c-a=y;c+a-b=z\)thì \(x+y+z=a+b+c;a=\frac{y+z}{2};b=\frac{z+x}{x};c=\frac{x+y}{2}\)
Ta cần chứng minh \(S=\text{∑}_{cyc}\frac{\left(y+z\right)\left(z+x\right)}{2z}\ge2\left(x+y+z\right)\)
Ta có:
\(S=\frac{\left(y+z\right)\left(z+x\right)}{2z}+\frac{\left(x+y\right)\left(y+z\right)}{2y}+\frac{\left(z+x\right)\left(x+y\right)}{2x}\)
\(=\frac{xy+yz+zx+z^2}{2z}+\frac{xy+zx+yz+y^2}{2y}+\frac{x^2+xy+zx+yz}{2x}\)