 giải nhanh bài 5 hộ mình với ĐANG CẦN GẤP
giải nhanh bài 5 hộ mình với ĐANG CẦN GẤP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1 because
2 as long as
3 although
4 so that
5 although
6 even if
7 until
8 while
9 because
10 Although

\(M=\left(\dfrac{\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right).\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{2\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
2. Ta có:
\(\sqrt{x}>0\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}+2}>0\) hay \(M>0\)
Lại có: \(M=\dfrac{\sqrt{x}+2-1}{\sqrt{x}+2}=1-\dfrac{1}{\sqrt{x}+2}< 1\)
\(\Rightarrow0< M< 1\Rightarrow M>M^2\)
1) Ta có: \(M=\left(\dfrac{\sqrt{x}}{x-4}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{\sqrt{x}+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-2}{2}\)
\(=\dfrac{2\sqrt{x}+2}{2\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)

Bài 1.2
1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
2) Ta có: \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}+1}{3-\sqrt{x}}-\dfrac{3-11\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3-11\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3-3+11\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)

Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)


Giả sử số thứ nhất chia 5 dư 1 thì số thứ năm chia năm dư 5
Hay số thứ năm chia hết cho 5
Tiếp tục giả sử với các trường hợp số thứ hai, ba,... chia năm dư 1
Ta cũng thu được trong 5 số ấy luôn có 1 số chia hết cho 5
Do đó tích của 5 số tự nhiên liên tiếp luôn chia hết cho 5
Vậy tích của 5 số tự nhiên liên tiếp luôn chia hết cho 5

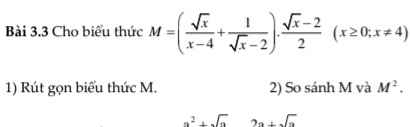







 Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha
Ai giải hộ mình bài 18 với! Mình đang cần gấp lắm :(( Cảm ơn trước nha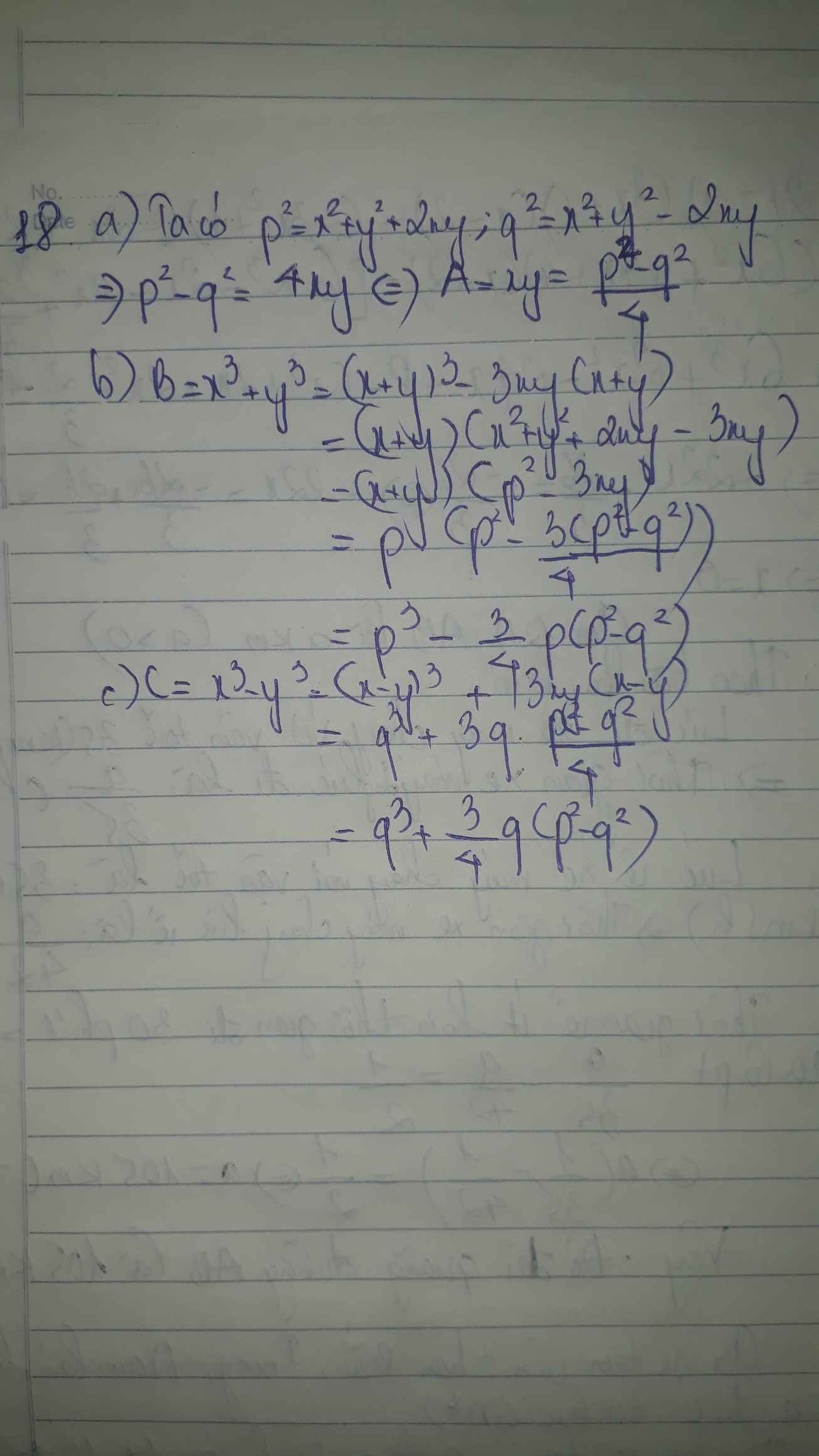
\(\dfrac{5}{42}:\dfrac{15}{7}+\dfrac{1}{2}\)
\(=\dfrac{5}{42}\times\dfrac{7}{15}+\dfrac{1}{2}\)
\(=\dfrac{1}{18}+\dfrac{1}{2}\)
\(=\dfrac{1}{18}+\dfrac{9}{18}=\dfrac{10}{18}=\dfrac{5}{9}\)
\(\rightarrow\) Chọn \(A.\dfrac{5}{9}\)
Câu 5:
\(\dfrac{5}{42}:\dfrac{15}{7}+\dfrac{1}{2}\)
\(=\dfrac{5}{42}\times\dfrac{7}{15}+\dfrac{1}{2}\)
\(=\dfrac{35}{630}+\dfrac{1}{2}=\dfrac{35}{630}+\dfrac{315}{630}=\dfrac{350}{630}=\dfrac{35}{63}=\dfrac{5}{9}\)
=>A