Rút gọn A = 5+42+43+...+499
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 4 2021
Bài 2:
b) Gọi \(d\inƯC\left(21n+4;14n+3\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}21n+4⋮d\\14n+3⋮d\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}42n+8⋮d\\42n+9⋮d\end{matrix}\right.\)
\(\Leftrightarrow1⋮d\)
\(\Leftrightarrow d\inƯ\left(1\right)\)
\(\Leftrightarrow d\in\left\{1;-1\right\}\)
\(\LeftrightarrowƯCLN\left(21n+4;14n+3\right)=1\)
hay \(\dfrac{21n+4}{14n+3}\) là phân số tối giản(đpcm)
3 tháng 4 2021
Bài 1:
a) Ta có: \(A=1+2-3-4+5+6-7-8+...-299-300+301+302\)
\(=\left(1+2-3-4\right)+\left(5+6-7-8\right)+...+\left(297+298-299-300\right)+301+302\)
\(=\left(-4\right)+\left(-4\right)+...+\left(-4\right)+603\)
\(=75\cdot\left(-4\right)+603\)
\(=603-300=303\)
4 tháng 4 2021
Bài 2:
a) Vì tổng của hai số là 601 nên trong đó sẽ có 1 số chẵn, 1 số lẻ
mà số nguyên tố chẵn duy nhất là 2
nên số lẻ còn lại là 599(thỏa ĐK)
Vậy: Hai số nguyên tố cần tìm là 2 và 599
4 tháng 4 2021
b,Gọi ƯCLN(21n+4,14n+3)=d
21n+4⋮d ⇒42n+8⋮d
14n+3⋮d ⇒42n+9⋮d
(42n+9)-(42n+8)⋮d
1⋮d ⇒ƯCLN(21n+4,14n+3)=1
Vậy phân số 21n+4/14n+3 là phân số tối giản
T
1
20 tháng 10 2021
\(\Rightarrow4A=4+4^2+4^3+...+4^{100}\\ \Rightarrow4A-A=\left(4+4^2+4^3+...+4^{100}\right)-\left(1+4+4^2+...+4^{99}\right)\\ \Rightarrow3A=4^{100}-1< 4^{100}=B\\ \Rightarrow A< \dfrac{B}{3}\)
MH
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
21 tháng 8 2023
\(4S=4+4^2+4^3+4^4+...+4^{100}\)
\(3S=4S-S=4^{100}-1\Rightarrow3S+1=4^{100}\)
Ta có \(32^{20}=\left(2^5\right)^{20}=2^{100}\)
\(\Rightarrow4^{100}>2^{100}\Rightarrow3S+1>32^{20}\)
12 tháng 8 2023
a)\(...A=\dfrac{2^{50+1}-1}{2-1}=2^{51}-1\)
b) \(...\Rightarrow B=\dfrac{3^{80+1}-1}{3-1}=\dfrac{3^{81}-1}{2}\)
c) \(...\Rightarrow C+1=1+4+4^2+4^3+...+4^{49}\)
\(\Rightarrow C+1=\dfrac{4^{49+1}-1}{4-1}=\dfrac{4^{50}-1}{3}\)
\(\Rightarrow C=\dfrac{4^{50}-1}{3}-1=\dfrac{4^{50}-4}{3}=\dfrac{4\left(4^{49}-1\right)}{3}\)
Tương tự câu d,e,f bạn tự làm nhé
PB
2
19 tháng 12 2021
\(S=\left(1+4\right)+\left(4^2+4^3\right)+...+\left(4^{98}+4^{99}\right)\\ S=\left(1+4\right)+4^2\left(1+4\right)+...+4^{98}\left(1+4\right)\\ S=\left(1+4\right)\left(1+4^2+...+4^{98}\right)=5\left(1+4^2+...+4^{98}\right)⋮5\)
19 tháng 12 2021
\(S=\left(1+4\right)+...+4^{98}\left(1+4\right)\)
\(=5\left(1+...+4^{98}\right)⋮5\)
19 tháng 5 2017
\(A=\frac{49^{24}.125^{10}.2^8-5^{30}.7^{49}.4^5}{5^{29}.16^2.7^{43}}\)
\(A=\frac{7^{48}.5^{30}.2^8-5^{30}.7^{49}.2^{10}}{5^{29}.2^8.7^{43}}\)
\(A=\frac{5^{30}.7^{48}.2^8.\left(1-7.2^2\right)}{5^{29}.2^8.7^{43}}=5.7^3.\left(1-7.2^2\right)=1715.\left(-27\right)=-46305\)
E
19 tháng 5 2017
\(A=\frac{\left(7^2\right)^{24}.\left(5^3\right)^{10}.2^8-5^{30}.7^{49}.\left(2^2\right)^5}{5^{29}\left(2^4\right)^2.7^{43}}=\frac{7^{48}.5^{30}.2^8-5^{30}.7^{49}.2^{10}}{5^{29}.2^8.7^{43}}=\frac{7^{48}.5^{30}.2^8\left(1-7.2^2\right)}{5^{29}.2^8.7^{43}}\)
=\(7^5.5.\left(-27\right)=-2268945\)
VI
5
MA
9 tháng 9 2016
Đặt: \(P=\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\)
\(P^2=\left(\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}\right)^2\)
\(P^2=94-42\sqrt{5}-2\sqrt{94-42\sqrt{5}}.\sqrt{94+42\sqrt{5}}+94+42\sqrt{5}\)
\(P^2=188-2\sqrt{\left(94-42\sqrt{5}\right)\left(94+42\sqrt{5}\right)}\)
\(P^2=188-2\sqrt{94^2+3948\sqrt{5}-3948\sqrt{5}-8820}\)
\(P^2=188-2\sqrt{8836-8820}\)
\(P^2=188-2\sqrt{16}\)
\(P^2=188-8\)
\(P^2=180\)
\(P=\orbr{\begin{cases}6\sqrt{5}\\-6\sqrt{5}\end{cases}}\) .
Mà theo bài ra: \(\sqrt{94-42\sqrt{5}}< \sqrt{94+42\sqrt{5}}\)
\(\Rightarrow\sqrt{94-42\sqrt{5}}-\sqrt{94+42\sqrt{5}}< 0\)
\(\Rightarrow P=-6\sqrt{5}\)
9 tháng 9 2016
Làm gì phức tạp thế
94 - 42\(\sqrt{5}\)= 49 - 2×7×3×\(\sqrt{5}\)+ 45 = (7 - \(3\sqrt{5}\))2
Tương tự 94 + 42\(\sqrt{5}\) = (7 + \(3\sqrt{5}\))2
Từ đó suy ra đáp số là 6\(\sqrt{5}\)
PT
1
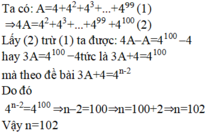
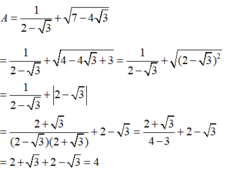
Ta giữ nguyên 5
2xA=4^3+4^4+...+4^100
2xA-A=(4^3+4^4+...+4^100-4^2+4^3+...+4^99)
A=4^100-4+5
A=4^100+1
Vậy A=4^100+1
Ta có : \(A=5+4^2+4^3+...+4^{99}\)
\(A-5=4^2+4^3+...+4^{99}\)
\(4\left(A-5\right)=4^3+4^4+...+4^{100}\)
\(4\left(A-5\right)-\left(A-5\right)=\left(4^3+4^4+...+4^{100}\right)-\left(4^2+4^3+...+4^{99}\right)\)
\(\Leftrightarrow3\left(A-5\right)=4^{100}-4^2\)
\(\Rightarrow A-5=\frac{4^{100}-4^2}{3}\)
\(\Rightarrow A=\frac{4^{100}-4^2}{3}+5\)