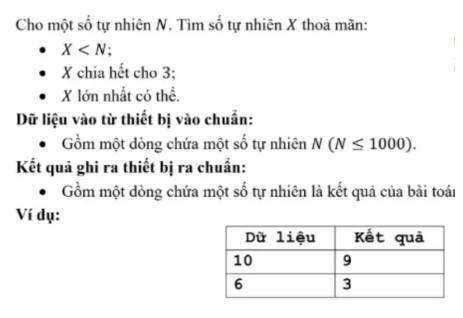
ai cứu với bằng c++ nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
30 tháng 4 2023
5,6 x 2 + 2,8 x 8 +11,2 x 2 - 50,4
= 5,6 x 2 + (2,8 x 2) x 4+ (11,2:2) x (2 x 2) - 50,4
= 5,6 x 2 + 5,6 x 4+ 5,6 x 4 - 5,6 x 9
= 5,6 x (2+4+4-9)
= 5,6 x 1= 5,6
10 tháng 4 2017
Ta có:
\(\frac{a}{b}=5\Leftrightarrow a=5b\)
\(a=b+272\Leftrightarrow a-b=272\)
Thay a=5b vào ta có:
\(5b-b=272\Leftrightarrow4b=272\)
\(\Leftrightarrow b=\frac{272}{4}=68\)
\(\Leftrightarrow a=5b=5\cdot68=340\)
Vậy số thứ nhất là 340 số thứ hai là 68
8 tháng 8 2023
\(B=\dfrac{3}{1x2}+\dfrac{3}{2x3}+...+\dfrac{3}{50x51}\)
\(B=3x\left(\dfrac{1}{1x2}+\dfrac{1}{2x3}+...+\dfrac{1}{50x51}\right)\)
\(B=3x\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{50}-\dfrac{1}{51}\right)\)
\(B=3x\left(1-\dfrac{1}{51}\right)=3x\dfrac{50}{51}=\dfrac{150}{51}\)
MA
25 tháng 9 2016
Gọi a, b, c lần lượt là số hc sinh giỏi của các lớp 6, 7, 8 và chúng tỉ lệ vs 5, 4, 3
\(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=\frac{b-c}{4-3}=40\)
\(\frac{b}{4}=40\Rightarrow b=160\)
\(\frac{c}{3}=40\Rightarrow c=120\)
\(\frac{a}{5}=40\Rightarrow a=200\)
tíc mình nha
25 tháng 9 2016
goi số học sinh 3 khối lần lượt là a,b,c
suy ra : a/5=b/4=c/3=k
suy ra a=5k b=4k c=3k
ta có 4k-3k=40
suy ra k=40
suy ra a=200 b=160 c=120
LT
1
AH
Akai Haruma
Giáo viên
22 tháng 12 2022
Lời giải:
4.
$29(19-13)-19(29-13)=29.19-29.13-(19.29-19.13)$
$=29.19-29.13-19.29+19.13=(29.19-19.29)-(29.13-19.13)$
$=0-13(29-19)=0-13.10=-130$
5.
$31(-18)+31(-81)-31=31[(-18)+(-81)-1]=31[-(18+81)-1]=31(-100)=-3100$
6.
$(-12).47+(-12).52+(-12)=(-12)(47+52+1)=(-12).100=-1200$
7.
$13(23+22)-3(17+28)=13.45-3.45=45(13-3)=45.10=450$
26 tháng 7 2017
\(\frac{2.4+2.4.8+4.8.16+8.16.32}{3.4+2.6.8+4.12.16+8.24.32}\)
=\(\frac{4.2+2.8.2.2+4.16.4.2+8.32.8.2}{4.3+2.8.2.3+4.16.4.3+8.32.8.3}\)
=\(\frac{2.\left(4+2.8.2+4.16.4+8.32.8\right)}{3.\left(4+2.8.2+4.16.4+8.32.8\right)}\)
=\(\frac{2}{3}\)
Ủng hộ mik nhé !!!
26 tháng 7 2017
Đặt biểu thức trên là A. Ta có:
A=\(\frac{2^3+2^6+2^9+2^{12}}{2^2.3+2^5.3+2^8.3+2^{11}.3}\)
=\(\frac{2^3.\left(1+2^3+2^6+2^9\right)}{2^2.3.\left(1+2^3+2^6+2^9\right)}\)
= \(\frac{2^3}{2^2.3}\)
=\(\frac{2}{3}\)
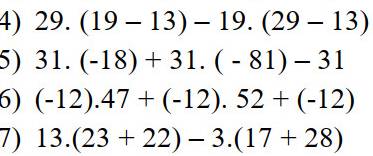
#include <bits/stdc++.h>
using namespace std;
#define nmax 1000007
long long a[nmax];
int main()
{
long long n;
cin>>n;
n--;
while(n%3!=0)
{
n--;
}
cout<<n;
}