| tìm giá trị nhỏ nhất của biểu thức sau | |
b=/2x-1/+/2x-2015/
| |
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
2
Những câu hỏi liên quan
14 tháng 7 2015
a)Ta có: |x+3|>=0
=>|x+3|+15>=15 hay A>=15
Nên GTNN của A là 15 khi:
x+3=0
x=0-3
x=-3
b)B=|2x+1|-2015
Ta có: |2x+1|>=0
=>|2x+1|-2015>=-2015 hay B>=-2015
Nên GTNN của B là -2015 khi:
2x+1=0
2x=0-1
x=-1/2
c)C=|3x-4|+|y-1|+17
Ta có: |3x-4|>=0
|y-1|>=0
=>|3x-4|+|y-1|+17>=17 hay C>=17
Nên GTNN của C là 17 khi:
3x-4=0 hay y-1=0
3x=0+4 y=0+1
x=4/3 y=1
HN
0
NA
5 tháng 9 2018
a) Vì |2x-1|\(\ge0\)
\(\Rightarrow A=\left|2x-1\right|+5\ge5\)
Dấu '=' xảy ra khi \(2x-1=0\)
\(\Leftrightarrow2x=1\Leftrightarrow x=\frac{1}{2}\)
Vậy Min A = 5 khi x =1/2
b)Vì \(\frac{1}{2}\left|x-1\right|\ge0\)
\(\Rightarrow B\ge3\)
Dấu '=' xảy ra khi x-1 =0
<=> x=1
Vậy Min B = 3 khi x =1
18 tháng 4 2020
a,Ta thấy \(x^2\ge0\) \(\left(\forall x\right)\)
\(\Rightarrow x^2+2015\ge2015\)
Dấu "=" xảy ra \(\Leftrightarrow x^2=0\)\(\Rightarrow x=0\)
Vậy Min \(x^2+2015=2015\)\(\Leftrightarrow x=0\)
b, Ta thấy \(\left(1-2x\right)^2\ge0\)\(\left(\forall x\right)\)
\(\Rightarrow\left(1-2x\right)^2-12\ge-12\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\left(1-2x\right)^2=0\)\(\Rightarrow1-2x=0\)\(\Rightarrow2x=0\Rightarrow x=0\)
Vậy Min \(\left(1-2x\right)^2-12=12\Leftrightarrow x=0\)
CM
9 tháng 2 2017
Q = x 2 + 2 y 2 + 2 x y − 2 x − 6 y + 2015 = x 2 + 2 x y + y 2 − 2 x − 2 y + 1 + y 2 − 4 y + 4 + 2010 = x 2 + 2 x y + y 2 − 2 x + 2 y + 1 + y 2 − 4 y + 4 + 2010 = x + y 2 − 2 x + y + 1 + y 2 − 4 y + 4 + 2010 = x + y − 1 2 + y − 2 2 + 2010
NA
0
18 tháng 3 2021
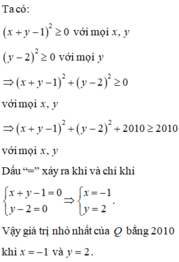
a) Ta có: \(\left(x-2\right)^2\ge0\forall x\)
nên Dấu '=' xảy ra khi x-2=0
hay x=2
Vậy: Gtnn của biểu thức \(\left(x-2\right)^2\) là 0 khi x=2
\(b=\left|2x-1\right|+\left|2x-2015\right|\)
Ta có \(\left|2x-1\right|\)và \(\left|2x-2015\right|\ge0\)với mọi \(x\)
\(\Rightarrow\)\(\left|2x-1\right|+\left|2x-2015\right|\ge0\)
\(\Rightarrow\)\(b\ge0\)
\(\Rightarrow\)Giá trị nhỏ nhất của b là 0 khi \(\left|2x-1\right|\)và \(\left|2x-2015\right|\)là hai số nguyên đối nhau
Vậy GTNN của b = 0
/ là dấu gì thế
dấu giá trị tuyệt đối à