CM \(\frac{a^4+b^4}{2}\ge\)ab3+ba3 -a2b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 8 2018
Phân tích
4 x 2 + 4 x + 4 - a x + b = 4 x 2 + 4 x + 1 - 2 x + 1 + 2 x + 1 - a x + b = 4 x 2 + 4 x + 1 - 2 x + 1 + 2 - a x + 1 - b
Ta có
lim x → ∞ 4 x 2 + 4 x + 3 - 2 x + 1 = lim x → ∞ 2 4 x 2 + 4 x + 3 - 2 x + 1
Khi đó
lim x → ∞ 4 x 2 + 4 x + 3 - a x + b lim x → ∞ 2 - a x + 1 - b = 0 ⇔ 2 - a = 0 1 - b = 0 ⇔ a = 2 b = 1
Suy ra
a
-
2
b
2018
3
a
2
+
a
b
3
+
b
a
3
=0
Đáp án A
AH
Akai Haruma
Giáo viên
17 tháng 6 2019
Lời giải:
Áp dụng BĐT Cauchy:
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{4}{a^2+b^2}=\frac{a^2+b^2}{a^2b^2}+\frac{4}{a^2+b^2}\geq 2\sqrt{\frac{a^2+b^2}{a^2b^2}.\frac{4}{a^2+b^2}}=\frac{4}{ab}=\frac{32(a^2+b^2)}{8ab(a^2+b^2)}(1)\)
Tiếp tục áp dụng BĐT Cauchy ngược dấu:
\(8ab(a^2+b^2)=4.(2ab).(a^2+b^2)\leq (2ab+a^2+b^2)^2=(a+b)^4(2)\)
Từ \((1);(2)\Rightarrow \frac{1}{a^2}+\frac{1}{b^2}+\frac{4}{a^2+b^2}\geq \frac{32(a^2+b^2)}{8ab(a^2+b^2)}\geq \frac{32(a^2+b^2)}{(a+b)^4}\) (đpcm)
Dấu "=" xảy ra khi $a=b$
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 2 2020
\(\frac{1}{1+a^2}+\frac{1}{1+b^2}\ge\frac{2}{1+ab}\Leftrightarrow\frac{2+a^2+b^2}{\left(1+a^2+b^2+a^2b^2\right)}\ge\frac{2}{1+ab}\)
\(\Leftrightarrow\left(1+ab\right)\left(2+a^2+b^2\right)\ge2a^2b^2+2a^2+2b^2+2\)
\(\Leftrightarrow ab\left(a^2+b^2-2ab\right)-\left(a^2+b^2-2ab\right)\ge0\)
\(\Leftrightarrow\left(ab-1\right)\left(a-b\right)^2\ge0\)
b/ \(\frac{1}{1+a^4}+\frac{1}{1+b^4}+\frac{2}{1+b^4}\ge\frac{2}{1+a^2b^2}+\frac{2}{1+b^4}\ge\frac{4}{1+ab^3}\)
\(\Rightarrow\frac{1}{1+a^4}+\frac{3}{1+b^4}\ge\frac{4}{1+ab^3}\)
Hoàn toàn tương tự: \(\frac{1}{1+b^4}+\frac{3}{1+c^4}\ge\frac{4}{1+bc^3}\); \(\frac{1}{1+c^4}+\frac{3}{1+a^4}\ge\frac{4}{1+a^3c}\)
Cộng vế với vế ta có đpcm
AQ
1
7 tháng 5 2019
Ta có:\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\ge0\forall a,b,c\)
\(\Leftrightarrow a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2\ge0\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)-2\left(ab+bc+ca\right)\ge0\)
\(\Leftrightarrow2\left(a^2+b^2+c^2\right)\ge2\left(ab+bc+ca\right)\)
\(\Leftrightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow a^2+b^2+c^2\ge2\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(a^4+b^4+c^4\ge\frac{\left(a^2+b^2+c^2\right)^2}{3}\ge\frac{4}{3}\)
\(\Rightarrow a^4+b^4+c^4\ge\frac{4}{3}\left(đpcm\right)\)
Dấu '=' xảy ra khi\(\hept{\begin{cases}a=b=c\\ab+bc+ca=2\end{cases}\Leftrightarrow a=b=c=\sqrt{\frac{2}{3}}}\)
VT
11 tháng 9 2017
bài 1)
ta có \(\left(a-b\right)^2+\left(a-1\right)^2+\left(b-1\right)^2\ge0\)
\(\Rightarrow a^2-2ab+b^2+a^2-2a+1+b^2-2b+1\ge0\)
=> \(a^2+b^2+1\ge ab+a+b\)
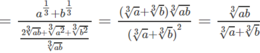
ta có:
\(\left(a^4-b^4\right)\left(a-b\right)\ge0\)
\(\Rightarrow a^5+b^5\ge a^4b+ab^4\Rightarrow a^5+a^4b+b^5+ab^4\ge2\left(a^4b+ab^4\right)=2ab\left(a^3+b^3\right)\)
\(\Rightarrow\left(a+b\right)\left(a^4+b^4\right)\ge2ab\left(a^3+b^3\right)\)
\(\Rightarrow a^4+b^4\ge2ab\left(a^2-ab+b^2\right)\Rightarrow\frac{a^4+b^4}{2}\ge ab^3+a^3b-a^2b^2\left(Q.E.D\right)\)