Cho \(\overline{abc+def}⋮37.\) Chứng minh \(\overline{abcdef⋮37}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(abc) chia hết cho 37
->100.a + 10.b + c chia hết cho 37
-> 1000.a + 100.b + 10.c chia hết cho 37
-> 1000.a - 999.a + 100.b + 10.c chia hết cho 37 (vì 999.a chia hết cho 37)
-> 100.b + 10.c + a = (bca) chia hết cho 37 (bca) chia hết cho 37
-> 100.b+10.c+a chia hết cho 37
-> 1000.b + 100.c + 10.a chia hết cho 37
-> 1000.b - 999.b + 100.c + 10.a chia hết cho 37 (vì 999.b chia hết cho 37)
-> 100.c + 10.a + b = (cab) chia hết cho 37

abc + def chia hết cho 37 ( theo đề bài ) => 1000 ( abc + def ) cũng chia hết 37
ta có : 1000 abc + 1000def <=> 1000abc + def + 999def
hay : abcdef + 999def ( chia hết cho 37 )
mà 999def chia hết cho 37 => abcdef cũng chia hết cho 37 => dpcm

abc+def = a*100000+b*10000+c*1000+d*100+e*10+f*1 = (a*b*c+d*e*f)*(100000+10000+1000+100+10+1) =(a*b*c+d*e*f)*111111 vì 111111 chia hết cho 37 nên (a*b*c+d*e*f) chia hết cho 37 => DPCM

Có: \(x+y\le\sqrt{2\left(x^2+y^2\right)}\) (dấu bằng xảy ra khi và chỉ khi x=y)
Đặt: \(\hept{\begin{cases}abc=x\\def=y\end{cases}}\)Như vậy x+y đạt GTLN khia và chỉ khi x=y do x không ràng buộc khác y
Thật vậy với x=y thì\(abcdef-defabc=0\)chia hết cho 2010
Vì x,y là 2 số tự nhiên có 3 chữ số khác nhau thức không ràng buộc x khác y
Nên: \(x=y=987\)
Max x+y=\(\sqrt{4\cdot987^2}=1974\)
Không viết đúng không
:v
Mình xem đáp án là 1328 với lại mình gõ nhầm;
abc, def là 2 số tự nhiên có 3 chữ số khác nhau. Biết abcdef - defabc chia hết cho 2010. Tìm giá trị lớn nhất của abc + def .

(abc) chia hết cho 37=> 100.a + 10.b + c chia hết cho 37
=> 1000.a + 100.b + 10.c chia hết cho 37
=> 1000.a - 999.a + 100.b + 10.c chia hết cho 37 (vì 999.a chia hết cho 37)
=> 100.b + 10.c + a = (bca) chia hết cho 37
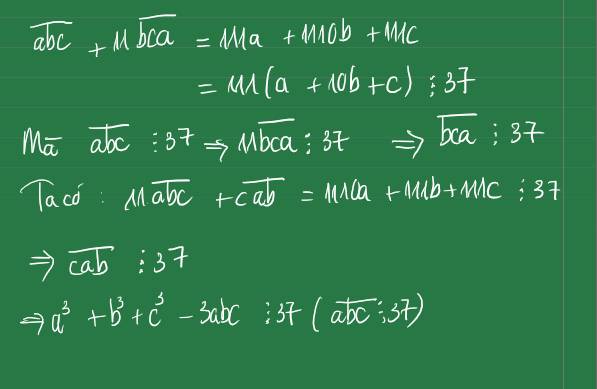
Ta có:
abcdef = 1000abc + def
Do (abc + def) ⋮ 37
Mà 37 là số nguyên tố
⇒ abc ⋮ 37 và def ⋮ 37
*) abc ⋮ 37
⇒ 1000abc ⋮ 37
⇒ (1000abc + def) ⋮ 37
⇒ abcdef ⋮ 37