b, 1/2. 5/6+ 2/3. 75%
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HA
1
Những câu hỏi liên quan
8 tháng 2 2021
a)\(\left(-3\right).8.\left(-2\right).5=\left(-3\right).\left(-2\right).8.5\)
\(=6.40=240\)
b)\(127-18.\left(5+6\right)=127-18.11\)
\(=127-198=-71\)
c)\(125-\left(-75\right)+32-\left(48+32\right)=125+75+32-48-32\)
\(\left(125+75\right)+\left(32-32\right)-48=200-48=152\)
d)\(3.\left(-4\right).2+2.\left(-5\right)-20=-12.2+2.\left(-5\right)-20\)
\(=\left(-12-5\right).2-20=-17.2-20=-140-20=-160\)
Chúc bạn học tốt
KV
3 tháng 12 2023
a) (38 - 60) + (20 - 38)
= 38 - 60 + 20 - 38
= (38 - 38) + (-60 + 20)
= 0 - 40
= -40
b) 75 - (20 + 75)
= 75 - 20 - 75
= (75 - 75) - 20
= 0 - 20
= -20
c) 32 + (60 - 32)
= 32 + 60 - 32
= (32 - 32) + 60
= 0 + 60
= 60
d) (81 - 36) - (81 - 36)
= 81 - 36 - 81 + 36
= (81 - 81) + (-36 + 36)
= 0 + 0
= 0
e) (2 + 4 + 6 + 8) - (1 + 3 + 5 + 7)
= 2 + 4 + 6 + 8 - 1 - 3 - 5 - 7
= (2 - 1) + (4 - 3) + (6 - 5) + (8 - 7)
= 1 + 1 + 1 + 1
= 4
f) (1 + 3 + 5 + 7 + ... + 99) - (2 + 4 + 6 + 8 + ... + 100)
= 1 + 3 + 5 + 7 + ... + 99 - 2 - 4 - 6 - 8 - ... - 100
= (1 - 2) + (3 - 4) + (5 - 6) + (7 - 8) + ... + (99 - 100)
= -1 - 1 - 1 - 1 - ... - 1 (50 chữ số 1)
= -50
27 tháng 6 2021
\(a,=-2\sqrt{5}+9\sqrt{5}-24\sqrt{5}-\sqrt{5}=-18\sqrt{5}\)
\(b,=2\sqrt{3}-5\sqrt{3}+4\sqrt{3}-7\sqrt{3}=-6\sqrt{3}\)
\(c,=3\sqrt{3}+7\sqrt{3}-9\sqrt{3}+11\sqrt{3}=12\sqrt{3}\)
27 tháng 6 2021
a) Ta có: \(-\sqrt{20}+3\sqrt{45}-6\sqrt{80}-\dfrac{1}{5}\sqrt{125}\)
\(=-2\sqrt{5}+9\sqrt{5}-24\sqrt{5}-\dfrac{1}{5}\cdot5\sqrt{5}\)
\(=-17\sqrt{5}-\sqrt{5}=-18\sqrt{5}\)
b) Ta có: \(2\sqrt{3}-\sqrt{75}+2\sqrt{12}-\sqrt{147}\)
\(=2\sqrt{3}-5\sqrt{3}+4\sqrt{3}-7\sqrt{3}\)
\(=-6\sqrt{3}\)
21 tháng 12 2023
Bài 1:
a: \(5\sqrt{8}-4\sqrt{27}-2\sqrt{75}+\sqrt{108}\)
\(=5\cdot2\sqrt{2}-4\cdot3\sqrt{3}-2\cdot5\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-12\sqrt{3}-10\sqrt{3}+6\sqrt{3}\)
\(=10\sqrt{2}-16\sqrt{3}\)
b: \(\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(1-\sqrt{6}\right)^2}\)
\(=\left|3-\sqrt{6}\right|+\left|1-\sqrt{6}\right|\)
\(=3-\sqrt{6}+\sqrt{6}-1\)
=3-1=2
c: \(\dfrac{5\sqrt{3}-3\sqrt{5}}{\sqrt{5}-\sqrt{3}}+\dfrac{1}{4+\sqrt{15}}\)
\(=\dfrac{\sqrt{15}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}+\dfrac{1\left(4-\sqrt{15}\right)}{16-15}\)
\(=\sqrt{15}+4-\sqrt{15}=4\)
d: \(\dfrac{2\sqrt{3-\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{10}-\sqrt{2}}-\dfrac{\sqrt{15}+\sqrt{5}}{\sqrt{12}+2}\)
\(=\dfrac{\sqrt{3-\sqrt{5}}\cdot\sqrt{2}\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}\left(\sqrt{3}+1\right)}{2\left(\sqrt{3}+1\right)}\)
\(=\dfrac{\sqrt{6-2\sqrt{5}}\cdot\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=\sqrt{\left(\sqrt{5}-1\right)^2}\cdot\dfrac{\left(3+\sqrt{5}\right)}{\sqrt{5}-1}-\dfrac{\sqrt{5}}{2}\)
\(=3+\sqrt{5}-\dfrac{\sqrt{5}}{2}=3+\dfrac{\sqrt{5}}{2}\)
Bài 2:
Vẽ đồ thị:
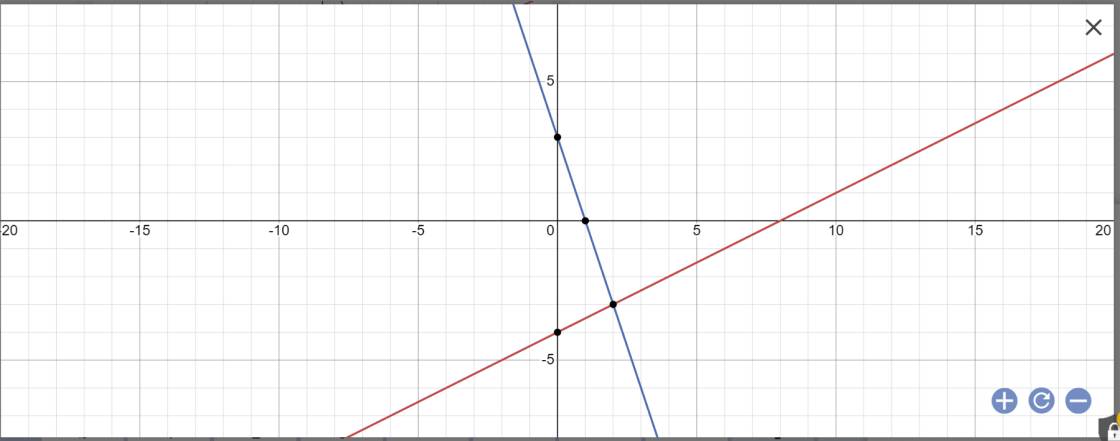
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x-4=-3x+3\)
=>\(\dfrac{1}{2}x+3x=3+4\)
=>\(\dfrac{7}{2}x=7\)
=>x=2
Thay x=2 vào y=-3x+3, ta được:
\(y=-3\cdot2+3=-3\)
Vậy: (d1) cắt (d2) tại A(2;-3)
23 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(\left(\dfrac{7}{8}-\dfrac{3}{4}\right)\cdot1\dfrac{1}{3}-\dfrac{2}{3}\cdot0,5\)
`=`\(\dfrac{1}{8}\cdot\dfrac{4}{3}-\dfrac{1}{3}\)
`=`\(\dfrac{1}{6}-\dfrac{1}{3}=-\dfrac{1}{6}\)
`b)`
\(\left(2+\dfrac{5}{6}\right)\div1\dfrac{1}{5}+\left(-\dfrac{7}{12}\right)\)
`=`\(\dfrac{17}{6}\div1\dfrac{1}{5}-\dfrac{7}{12}\)
`=`\(\dfrac{85}{36}-\dfrac{7}{12}=\dfrac{16}{9}\)
`c)`
\(75\%-1\dfrac{1}{2}+0,5\div\dfrac{5}{12}\)
`=`\(-\dfrac{3}{4}+\dfrac{6}{5}=\dfrac{9}{20}\)
VN
Võ Ngọc Phương
VIP
23 tháng 7 2023
a) \(\left(\dfrac{7}{8}-\dfrac{3}{4}\right).1\dfrac{1}{3}-\dfrac{2}{3}.0,5\)
\(=\left(\dfrac{7}{8}-\dfrac{6}{8}\right).\dfrac{4}{3}-\dfrac{2}{3}.\dfrac{1}{2}\)
\(=\dfrac{1}{8}.\dfrac{4}{3}-\dfrac{2}{3}.\dfrac{1}{2}\)
\(=\dfrac{1}{6}-\dfrac{1}{3}\)
\(=\dfrac{-1}{6}\)
b) \(\left(2+\dfrac{5}{6}\right):1\dfrac{1}{5}+\dfrac{-7}{12}\)
\(=\left(\dfrac{12}{6}+\dfrac{5}{6}\right):\dfrac{6}{5}+\dfrac{-7}{12}\)
\(=\dfrac{17}{6}.\dfrac{5}{6}+\dfrac{-7}{12}\)
\(=\dfrac{85}{36}+\dfrac{-7}{12}\)
\(=\dfrac{16}{9}\)
c) \(75\%-1\dfrac{1}{2}+0,5:\dfrac{5}{12}\)
\(=\dfrac{3}{4}-\dfrac{3}{2}+\dfrac{1}{2}.\dfrac{12}{5}\)
\(=\dfrac{3}{4}-\dfrac{6}{4}+\dfrac{6}{5}\)
\(=\dfrac{-3}{4}+\dfrac{6}{5}\)
\(=\dfrac{9}{20}\)
4 tháng 8 2022
a: \(=\left(2\sqrt{6}-4\sqrt{3}+5\sqrt{2}-\dfrac{1}{2}\sqrt{2}\right)\cdot5\sqrt{6}\)
\(=\left(2\sqrt{6}-4\sqrt{3}+\dfrac{9}{2}\sqrt{2}\right)\cdot5\sqrt{6}\)
\(=60-20\sqrt{18}+\dfrac{45}{2}\sqrt{12}\)
\(=60-60\sqrt{2}+45\sqrt{3}\)
b: \(=\dfrac{\sqrt{5}+\sqrt{2}+\sqrt{5}-\sqrt{2}+3}{3}\cdot\dfrac{1}{3+2\sqrt{2}}\)
\(=\dfrac{2\sqrt{5}+3}{3}\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{2\sqrt{5}+3}{9+6\sqrt{2}}\)
25 tháng 6 2022
a: \(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{-8+15}{18}:17\)
\(=\dfrac{2}{3}+\dfrac{1}{3}\cdot\dfrac{7}{18}\cdot\dfrac{1}{17}\)
\(=\dfrac{619}{918}\)
b: \(=\left(3-7+\dfrac{1}{4}\right)\cdot\left(4-\dfrac{31}{6}+\dfrac{9}{4}\right)\)
\(=\dfrac{-15}{4}\cdot\dfrac{13}{12}=\dfrac{-195}{48}=\dfrac{-65}{16}\)
c: \(=\dfrac{3}{4}-\dfrac{3}{2}+\dfrac{1}{2}\cdot\dfrac{12}{5}-\dfrac{1}{4}\)
\(=\dfrac{1}{2}-\dfrac{3}{2}+\dfrac{6}{5}=\dfrac{6}{5}-1=\dfrac{1}{5}\)
d: \(=\dfrac{5}{4}\cdot\dfrac{1}{4}:\left(\dfrac{21}{16}-\dfrac{3}{2}\right)\)
\(=\dfrac{5}{16}:\dfrac{-3}{16}=\dfrac{-5}{3}\)
\(\dfrac{1}{2}\cdot\dfrac{5}{6}+\dfrac{2}{3}\cdot75\%\)
\(=\dfrac{1}{2}\cdot\dfrac{5}{6}+\dfrac{2}{3}\cdot\dfrac{3}{4}\)
\(=\dfrac{1\cdot5+2\cdot3}{12}=\dfrac{5+6}{12}=\dfrac{11}{12}\)