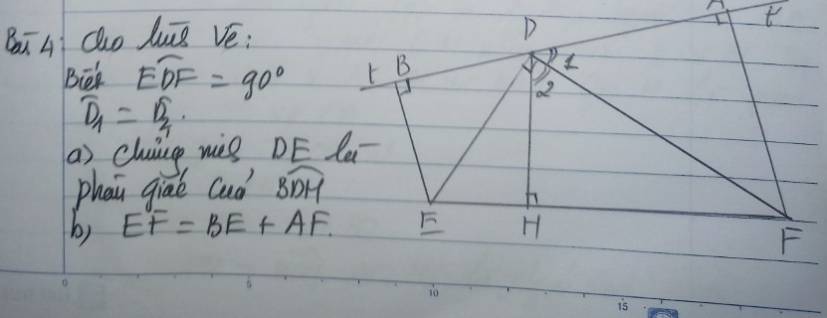
cho hình vẽ: bt EDF = 90 độ
Góc D1 =D2
a) DE LÀ PHÂN GIÁC CỦA GÓC BDM
B) È=BE+AF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho tam giác ABC có góc A = 120 độ . các đường phân giác AD,BE,CF
a, chứng minh rằng DE là phân giác góc ADC
b, EDF =90 độ
bài làm
hình ảnh tượng trưng cho em dễ tưởng tượng thôi đấy nhé ![[IMG]](http://diendan.hocmai.vn/images/smilies/khi/khi%20%28131%29.gif)
![[IMG]](http://nu5.upanh.com/b2.s34.d3/059526849fa4de3f4758f2528d9fb4a7_52953705.untitled.bmp)
_________
a)
chị gợi ý nhé :
vì AD là tia phân giác của góc A nên
BAD^=CAD^=60oBAD^=CAD^=60o
=> góc ngoài của đỉnh A = 180 - 120 = 60
__
theo t/c của 3 đường phân giác thì 3 đường đều giao tại 1 điểm
mà em có BE là tia P.G trong
AE là tia phân giác ngoài đỉnh A
2 tia này đã giao với nhau vậy => DE giao với 3 tia này => đpcm
là gợi ý thôi em nhé, em đừng chép lời vào kẻo bị đánh giá về ngôn ngữ toán học đấy
b)
cm DF là tia phân giác ngoài của tam giác ADC ,
=> góc EDF =90 độ
___
từ phần a => BED^=EDC^−EBD^BED^=EDC^−EBD^
= ADC^−ABC^2=BAD2ADC^−ABC^2=BAD2
__________________

a: Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
góc BAD=góc EAD
=>ΔABD=ΔAED
=>AB=AE
b: AB=AE
DB=DE
=>AD là trung trực của BE
a.
Ta có: \(\widehat{BDE}+\widehat{EDF}+\widehat{D_1}=180^0\)
\(\Rightarrow\widehat{BDE}+90^0+\widehat{D_1}=180^0\)
\(\Rightarrow\widehat{BDE}+\widehat{D_1}=90^0\)
Mà \(\widehat{D_1}=\widehat{D_2}\Rightarrow\widehat{BDE}+\widehat{D_2}=90^0\)
Lại có \(\widehat{HDE}+\widehat{D_2}=\widehat{EDF}=90^0\)
\(\Rightarrow\widehat{BDE}=\widehat{HDE}\)
\(\Rightarrow DE\) là phân giác của \(\widehat{BDH}\)
b.
Xét hai tam giác vuông BDE và HDE có:
\(\left\{{}\begin{matrix}DE-chung\\\widehat{BDE}=\widehat{HDE}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta_{\perp}BDE=\Delta_{\perp}HDE\left(ch-gn\right)\)
\(\Rightarrow BE=HE\)
Tương tự, xét 2 tam giác vuông HDF và ADF có:
\(\left\{{}\begin{matrix}DF-chung\\\widehat{D_2}=\widehat{D_1}\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta_{\perp}HDF=\Delta_{\perp}ADF\left(ch-gn\right)\)
\(\Rightarrow AF=HF\)
\(\Rightarrow HE+HF=BE+AF\)
\(\Rightarrow EF=BE+AF\)