tìm phân số tối giản bằng phân số 212121 phần 151515
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\frac{151515}{353535}=\frac{151515\div10101}{353535\div10101}=\frac{15}{35}\)

a, - 151515 / 232323 = -15/23
b, 1.2.3 + 2.4.6 + 4.8.12 / 1.3.5 + 2.4.6 + 4.12.20
= 146/341

A) Các phân số tối giản là : 3/4; 1/5
B) Các phân số chưa tối giản là : 20/100 = 1/5 ; 36/216 = 1/6 ; 15/90 = 1/6 ; 50/2010 = 5/201 ; 27/36 = 9/12
Mình chỉ làm phần A và B thôi nha

a) Các phân số tối giản là: \(\dfrac{9}{11};\dfrac{16}{23};\dfrac{91}{100}\)
b) \(\dfrac{7}{14}=\dfrac{7:7}{14:7}=\dfrac{1}{2};\dfrac{15}{24}=\dfrac{15:3}{24:3}=\dfrac{5}{8};\dfrac{64}{80}=\dfrac{64:16}{80:16}=\dfrac{4}{5}\)
a) Các phân số tối giản: \(\dfrac{9}{11};\dfrac{16}{23};\dfrac{91}{100}\)
b) \(\dfrac{7}{14}=\dfrac{7:7}{14:7}=\dfrac{1}{2}\) ; \(\dfrac{15}{24}=\dfrac{15:3}{24:3}=\dfrac{5}{8}\) ; \(\dfrac{64}{80}=\dfrac{64:16}{80:16}=\dfrac{4}{5}\)

220 = 4. 5. 11 nên ta có các phân số tối giản sau đây thỏa mãn các điều kiện của bài toán:
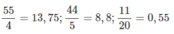

gọi d là ƯC(3n - 2; 4n - 3)
\(\Rightarrow\hept{\begin{cases}3n-2⋮d\\4n-3⋮d\end{cases}\Rightarrow\hept{\begin{cases}4\left(3n-2\right)⋮d\\3\left(4n-3\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}12n-8⋮d\\12n-9⋮d\end{cases}}}\)
\(\Rightarrow12n-8-12n+9⋮d\)
\(\Rightarrow1⋮d\)
\(\Rightarrow d=\pm1\)
=> ...

Gọi phân số tối giản là \(\frac{a}{b}\)
=> Phân số cần tìm là \(\frac{7xa}{7xb}\)
Theo đề bài
\(7xax7xb=49xaxb=490\Rightarrow axb=10\)
\(\Rightarrow a=10\Rightarrow b=1\) hoặc \(a=5\Rightarrow b=2\)
Suy ra phân số cần tìm là \(\frac{70}{7}\) hoặc \(\frac{35}{14}\)
212121/151515 = 212121 : 30303/151515 : 30303 = 7/5