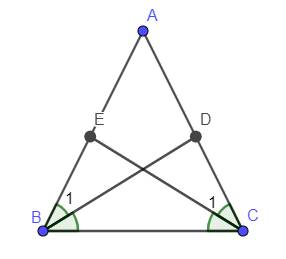
Cho tam giác ABC cân tại A , các đường phân giác BD ; CE ( D thuộc AC ; E thuộc AB ) . C/m BDEC - httg cân có đáy nhỏ bên bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 8 2016
Tam giác BCD có HE là đường trung bình HE = BD/2 = AH
Tam giác AEH cân tại H ⇒ ∠AEH = ∠EAH = ∠BAC/2
∠AHE = 180° - ∠AEH - ∠EAH = 180° - ∠BAC
∠CBD = ∠CHE = 90° - ∠AHE = 90° - (180° - ∠BAC) = ∠ABC - 90°
∠ACB = ∠ABC = 2∠CBD = 2∠BAC - 180°
∠ACB + ∠ABC + ∠BAC = 5∠BAC - 360° = 180° ⇒ ∠BAC = 108°
N
Cho tam giác ABC cân tại A, đường cao AH, đường phân giác BD. Tính các góc của tam giác biết BD=2AH.
0
S2
0
12 tháng 3 2023
Có `Delta ABC` cân tại `A=>AB=AC;hat(ABC)=hat(ACB)`
Có `hat(ABC)=hat(ACB)(cmt)`
mà `BD` là p/g `hat(ABC)`
`CE` là p/g `hat(ACB)`
nên `hat(B_1)=hat(C_1)`
Xét `Delta ABD` và `Delta ACE` có :
`{:(hat(B_1)=hat(C_1)(cmt)),(AB=AC(cmt)),(hat(A)-chung):}}`
`=>Delta ABD=Delta ACE(g.c.g)`
`=>BD=CE` ( 2 cạnh t/ứng )(đpcm)
13 tháng 3 2023
A B C D E
BD là đường phân giác của góc B nên ta có :
\(\widehat{ABD}=\widehat{CBD}=\dfrac{1}{2}\widehat{B}\) ( 1 )
CE là đường phân giác của góc C nên ta có :
\(\widehat{ACE}=\widehat{BCE}=\dfrac{1}{2}\widehat{C}\) ( 2 )
Từ ( 1 ) , ( 2 ) = > \(\widehat{ABD}=\widehat{ACE}\)
Xét tam giác ADB và tam giác AEC ta có :
Góc A chung
AB = AC ( gt )
\(\widehat{ABD}=\widehat{ACE}\) ( cmt )
= > \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
= > BD = CE ( 2 cạnh tương ứng )
27 tháng 1 2017
A B C M D K
từ M vẽ MK// BD ( K thuộc AC )
Tam giác BDC có : M là trung điểm BC; MK//BD
Suy ra : K là trung điểm CD
Do đó: MK là đường trung bình của tam giác BDC.
--> MK = BD/2 = 2AM/2 = AM
---> tam giác AMK cân tại M --> góc MAK = góc MKA
Ta có : góc MAK + góc C = 90 độ
hay góc MKA + góc C = 90 độ
==> góc MKA = 90 độ - góc C (1)
Lại có : góc MKA = góc KMC + góc C = góc DBC + góc C = góc B/2 + góc C = góc C/2 + góc C = 3/2. góc C (2)
Từ (1) (2) ==> 90 độ - góc C = 3/2. góc C
==> 5/2. góc C = 90 độ
==> góc C = 36 độ
==> góc B = 36 độ
==> góc A= 180-36.2=108 độ
Hình thì tự đọc điều kiện rồi vẽ nha :)
* Xét t/g ABD và t/g ACE có :
AB = AC ( t/g ABC cân tại A )
\(\widehat{A}\) chung
\(\widehat{B2}\)\(=\)\(\widehat{C2}\)\(\left(\widehat{B2}=\frac{\widehat{ABC}}{2};\widehat{C2}=\frac{\widehat{ACB}}{2};\widehat{ABC}=\widehat{ACB}\right)\)
\(\Rightarrow\)t/g ABD = t/g ACE ( g-c-g )
\(\Rightarrow\)AD = AE
\(\Rightarrow\)t/g ADE cân tại A
\(\Rightarrow\)\(\widehat{E1}\)\(=\)\(\frac{180-\widehat{A}}{2}\) ( Vì t/g ABC cân tại A )
\(\widehat{ABC}\)\(=\)\(\frac{180-\widehat{A}}{2}\) ( Vì t/g ABC cân tại A )
\(\Rightarrow\)\(\widehat{E1}\)\(=\)\(\widehat{ABC}\)( và ở vị trí đồng vị )
\(\Rightarrow\)ED // BC
\(\Rightarrow\)BDEC - hình thang
Ta có : \(\widehat{ABC}\)\(=\)\(\widehat{ACB}\)
\(\Rightarrow\)BDEC - hình thang cân
\(\widehat{D1}=\widehat{B1}\) ( so le trong ; ED // BC )
\(\widehat{B2}=\widehat{B1}\) ( gt )
\(\Rightarrow\)\(\widehat{D1}=\widebat{B2}\)
\(\Rightarrow\)t/g BED cân tại A
\(\Rightarrow\)BE = ED
có ai làm đc bà này ko :)