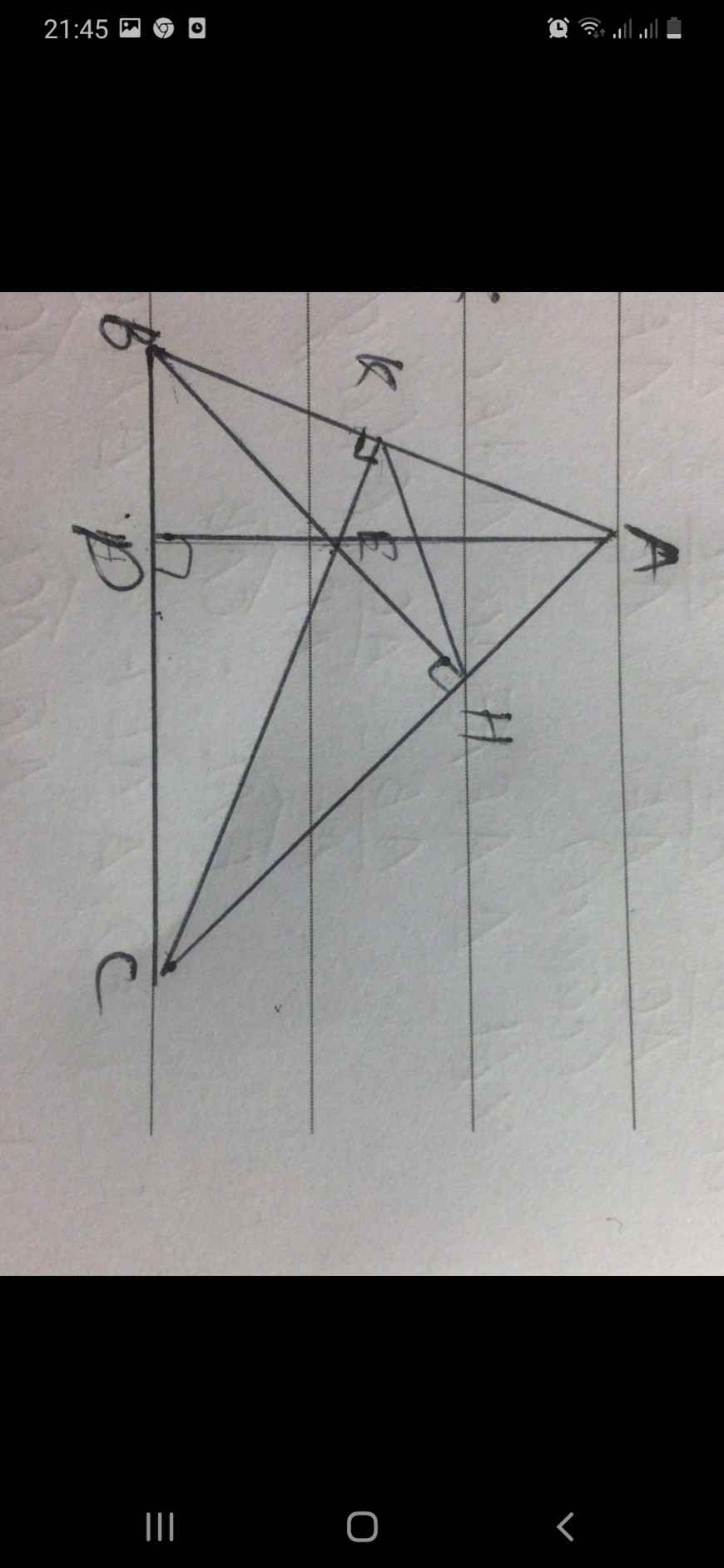
Cho tam giác ABC có góc A=2 góc B .Chứng Minh BC2=AC (AC+AB)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2021
1) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Suy ra: \(\dfrac{HB}{AB}=\dfrac{AB}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)
2 tháng 4 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
\(\widehat{BAH}\) chung
Do đó: ΔABH\(\sim\)ΔACK
b: Xét ΔKEB vuông tại K và ΔHEC vuông tại H có
\(\widehat{KEB}=\widehat{HEC}\)
DO đó: ΔKEB\(\sim\)ΔHEC
Suy ra: EK/EH=EB/EC
hay \(\dfrac{EK}{EB}=\dfrac{EH}{EC}\)
c: Xét ΔAKH và ΔACB có
AK/AC=AH/AB
góc A chung
Do đó: ΔAKH\(\sim\)ΔACB
Suy ra: \(\widehat{AKH}=\widehat{ACB}\)
17 tháng 4 2023
a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng vơi ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: \(DB=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{BAC}=\dfrac{1}{2}\cdot4\cdot6=12\left(cm^2\right)\)
4 tháng 12 2016
Mình làm câu A thôi nha:
Xét tam giác ADB và tam giác ADC
Ta có:AB=AC (gt)
góc A1=A2 (gt)
AD là cạnh chung
=>tam giác ADB=tam giác ADC (cạnh-góc-cạnh)
18 tháng 12 2016
Xét AHD và AKD lần lượt vuông tại H,K có:
AD: cạnh chung
HAD = KAD ( vì AD là tia phân giác góc A)
Suy ra AHD=AKD(ch-gn)
Do đó AH=AK ( 2 cạnh tương ứng)