Cho tam giác ABC có G là trọng tâm. Phân tích BA theo BC và GC
Giải chi tiết cho mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có trung tuyến BM và trọng tâm G . Phân tích vecto BG theo hai vecto BA và vecto BC

\(\overrightarrow{BG}=\dfrac{2}{3}\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\)

A B M C D H H
Gọi G là trọng tâm của tam giác ABC\(\frac{\Rightarrow AG}{AM}=\frac{2}{3}\)
Ta có \(\hept{\begin{cases}BM=CM\\\widehat{BHM}=\widehat{CKM}=90^0\\\widehat{BMH}=\widehat{CMK}\end{cases}\Rightarrow\Delta BHM=\Delta CKM\left(\text{ cạnh huyền - góc nhọn}\right)}\)
Vì vậy \(HM=KM\) nên AM là trung tuyến của \(\Delta AHK\) mà \(\frac{AG}{AM}=\frac{2}{3}\Rightarrow G\) là trọng tâm tam giác AHK

a, Ta có:AM+AN=OM-OA+ON-OA=OM+ON+AC=OC+AC=3/2OC
GA+3GB+GC+OD=2GB+OD=OB+OD=0
C,

Chọn C.
Vì ![]() nên
nên
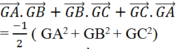
Gọi M, N, P lần lượt là trung điểm của BC, CA, AB
Tam giác ABM đều nên ![]()
Theo định lý Pitago ta có:
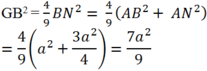
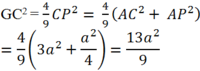
Suy ra
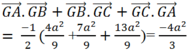
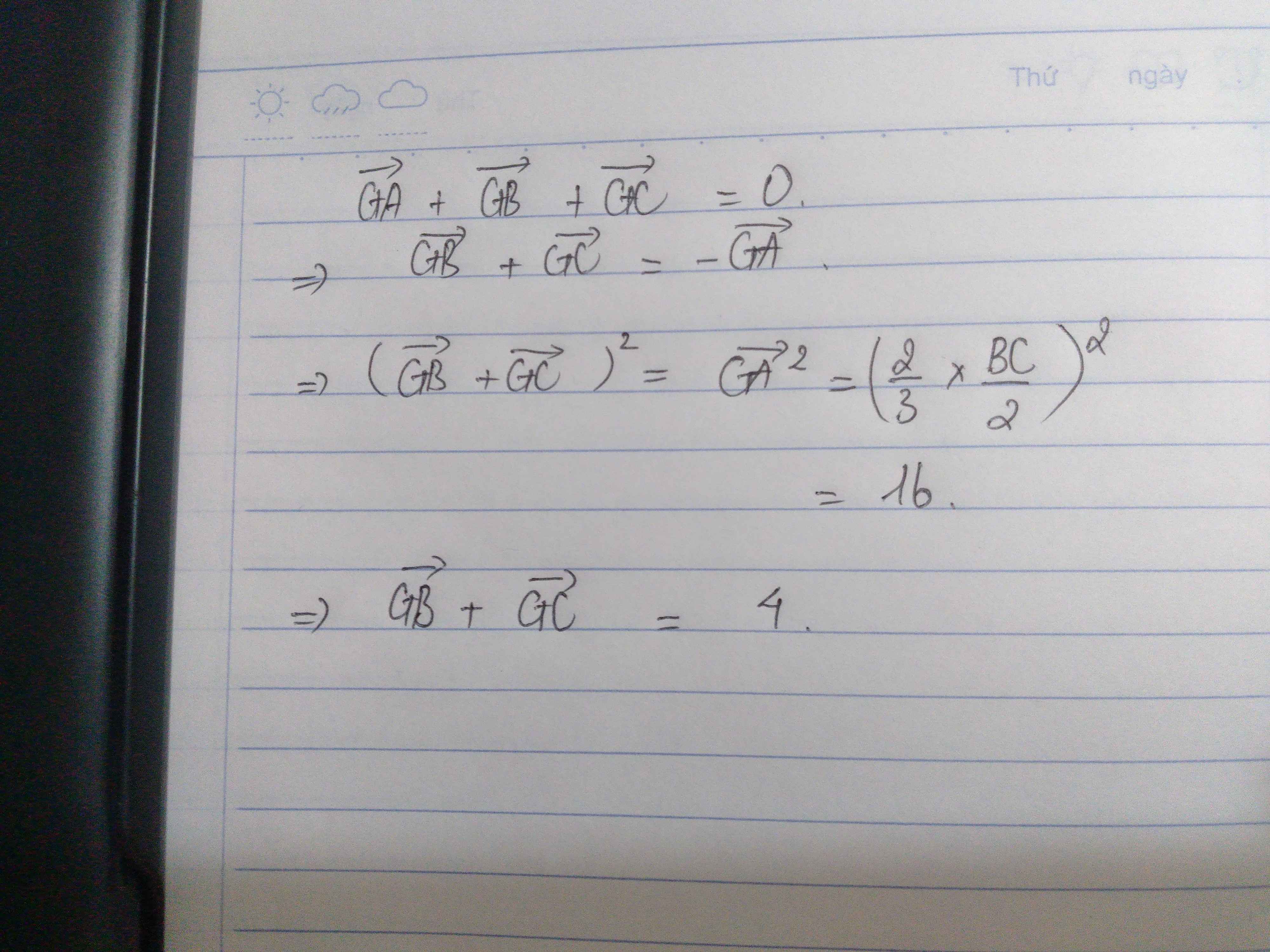
Lời giải:
Gọi $AE$ là đường trung tuyến của tam giác $ABC$ thì $E$ là trung điểm của $BC$
\(\overrightarrow{BA}=\overrightarrow{BC}+\overrightarrow{GA}=\overrightarrow{BC}+2\overrightarrow{EG}\\ =\overrightarrow{BC}+2(\overrightarrow{EC}+\overrightarrow{CG})\\ =\overrightarrow{BC}+2\overrightarrow{EC}+2\overrightarrow{CG}\\ =\overrightarrow{BC}+\overrightarrow{BC}-2\overrightarrow{GC}\\ =2\overrightarrow{BC}-2\overrightarrow{GC}\)