Cho tam giác ABC có trung tuyến AM và I là trung điểm của AM. Chứng minh rằng: a) IB+IC= AM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1 2016
hình tự vẽ nha bn
ta có MI//AC,M la tđ của BC=> I là tđ của AB
MK//AB,M la tđ của BC=> K là tđ của AC
tam giác ABM có N la tđ của AM,I là tđ cua AB=> IN la đtb của tam giác ABM=> NI//BM=> NI//BC(M thuộc BC) (1)
tương tự NK là đtb của tam giác AMC=> NK//MC=> NK//BC (M thuộc BC) (2)
từ (1),(2)=> NI và NK trùng nhau
=> 3 điểm I,N,K thẳng hàng
ta có MK//AI (MK//AB),IM//AK (IM//AC)=> tứ giác AKMI là hbh
tứ giác AKMI là hbh => 2 đg chéo IK và AM cắt nhau tại tđ mỗi đg
mà N là tđ của AM=> N là tđ của IK
21 tháng 12 2021
a: Xét tứ giác ADBM có
I là trung điểm của AB
I là trung điểm của DM
Do đó: ADBM là hình bình hành
mà AM=BM
nên ADBM là hình thoi
4 tháng 8 2023
a: Xét ΔABC có
E,F lần lượt là trung điểm của AB,AC
=>EF là đường trung bình
b: EF là đường trung bình
=>EF=BC/2=5cm
c: Xét ΔABC có
M,F lần lượt là trung điểm của CB,CA
=>MF là đường trung bình
=>MF=1/2AB và ME//AB
=>MF//AE và MF=AE
=>AEMF là hình bình hành
=>I là trung điểm của EF
=>EI=IF=EF/2=2,5cm
2 tháng 12 2023
a: Xét ΔAIM và ΔBIC có
IA=IB
\(\widehat{AIM}=\widehat{BIC}\)
IM=IC
Do đó: ΔAIM=ΔBIC
=>\(\widehat{IAM}=\widehat{IBC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AM//BC
ΔIAM=ΔIBC
=>AM=BC
b: Xét ΔEAN và ΔECB có
EA=EC
\(\widehat{AEN}=\widehat{CEB}\)
EN=EB
Do đó: ΔEAN=ΔECB
=>\(\widehat{EAN}=\widehat{ECB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//CB
c: ΔEAN=ΔECB
=>AN=CB
AN//CB
AM//CB
AN,AM có điểm chung là A
Do đó: M,A,N thẳng hàng
mà MA=NA
nên A là trung điểm của MN
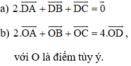
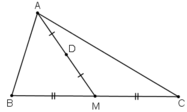
Ta có:
\(\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IM}\) (1)
Mặt khác: I là trung điểm AM
\(\Rightarrow\overrightarrow{AM}=2\overrightarrow{IM}\) (2)
Từ (1) và (2)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{AM}\)