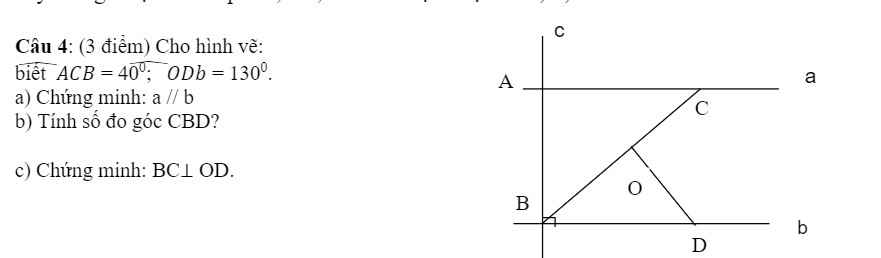
 Giúp mk c15 c16 vs ạ
Giúp mk c15 c16 vs ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
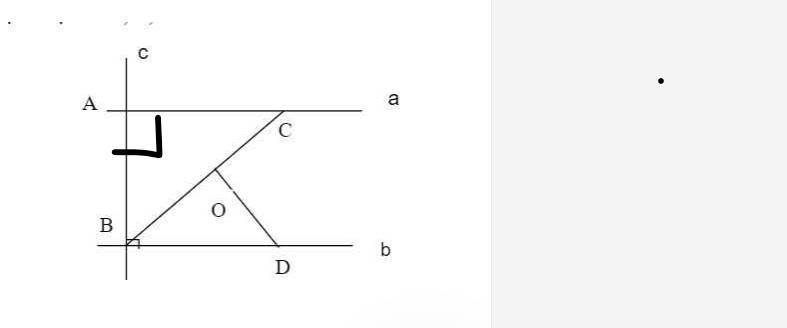
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC

a: Ta có: \(\widehat{DAH}+\widehat{DAB}=180^0\)
\(\widehat{CBK}+\widehat{CBA}=180^0\)
mà \(\widehat{DAB}=\widehat{CBA}\)
nên \(\widehat{DAH}=\widehat{CBK}\)
Xét ΔDAH vuông tại H và ΔCBK vuông tại K có
DA=CB
\(\widehat{DAH}=\widehat{CBK}\)
Do đó: ΔDAH=ΔCBK
Suy ra: AH=BK
b: Xét tứ giác HKCD có
HK//CD
HD//KC
Do đó: HKCD là hình bình hành
Suy ra: HK=CD
mà CD=10cm
nên HK=10cm
\(\Leftrightarrow AH=BK=\dfrac{HK-AB}{2}=\dfrac{10-6}{2}=2cm\)

a: Ta có: M và E đối xứng nhau qua AB
nên AB là đường trung trực của ME
Suy ra: AM=AE(1)
Ta có: M và F đối xứng nhau qua AC
nên AC là đường trung trực của MF
Suy ra: AM=AF(2)
Từ (1) và (2) suy ra AE=AF
b: Xét ΔAME có AM=AE
nên ΔAME cân tại A
mà AB là đường trung trực ứng với cạnh đáy ME
nên AB là tia phân giác của \(\widehat{MAE}\)
Xét ΔAMF có AM=AF
nên ΔAMF cân tại A
mà AC là đường trung trực ứng với cạnh đáy MF
nên AC là tia phân giác của \(\widehat{MAF}\)
Ta có: \(\widehat{EAF}=\widehat{FAM}+\widehat{EAM}\)
\(=2\cdot\left(\widehat{BAM}+\widehat{CAM}\right)\)
\(=2\cdot90^0=180^0\)
Do đó: E,A,F thẳng hàng
mà AE=AF
nên A là trung điểm của EF

Ta có: ΔABC cân tại A
mà AH là đường phân giác ứng với cạnh BC
nên AH là đường trung trực ứng với cạnh BC
Ta có: AE+EB=AB
AF+FC=AC
mà AE=AF
và AB=AC
nên EB=FC
Xét ΔEBH và ΔFCH có
EB=FC
\(\widehat{B}=\widehat{C}\)
HB=HC
Do đó: ΔEBH=ΔFCH
Suy ra: HE=HF
Ta có: AE=AF
nên A nằm trên đường trung trực của EF(1)
ta có: HE=HF
nên H nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra AH là đường trung trực của FE
hay E và F đối xứng nhau qua AH

Ta có: DB=DC
nên D nằm trên đường trung trực của BC(1)
Ta có: AB=AC
nên A nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra AD là đường trung trực của BC
hay B và C đối xứng nhau qua AD



\(a,=4x^2+12x+9\\ b,=2x^2-\dfrac{2}{3}xy+\dfrac{1}{3}y^2\\ c,=\left(7x-1\right)^2+\left(7x+1\right)^2+2\left(7x-1\right)\left(7x+1\right)\\ =\left(7x-1+7x+1\right)^2=196x^2\\ d,=\left[\left(x+3\right)^2-y^2\right]:\left(x+y+3\right)\\ =\left(x+y+3\right)\left(x-y+3\right):\left(x+y+3\right)=x-y+3\)
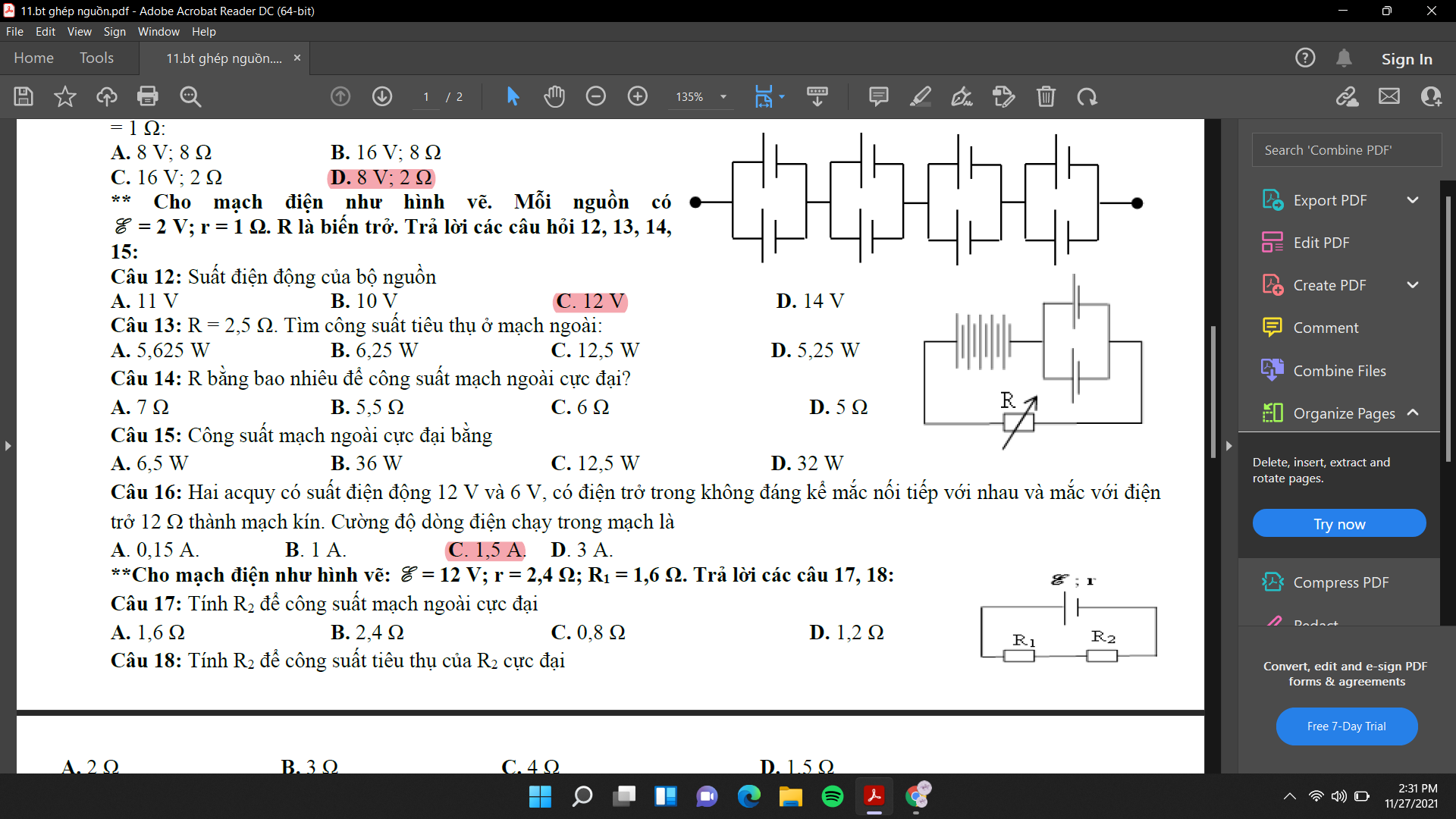
 mk vs ạ
mk vs ạ



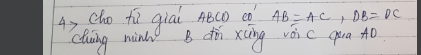

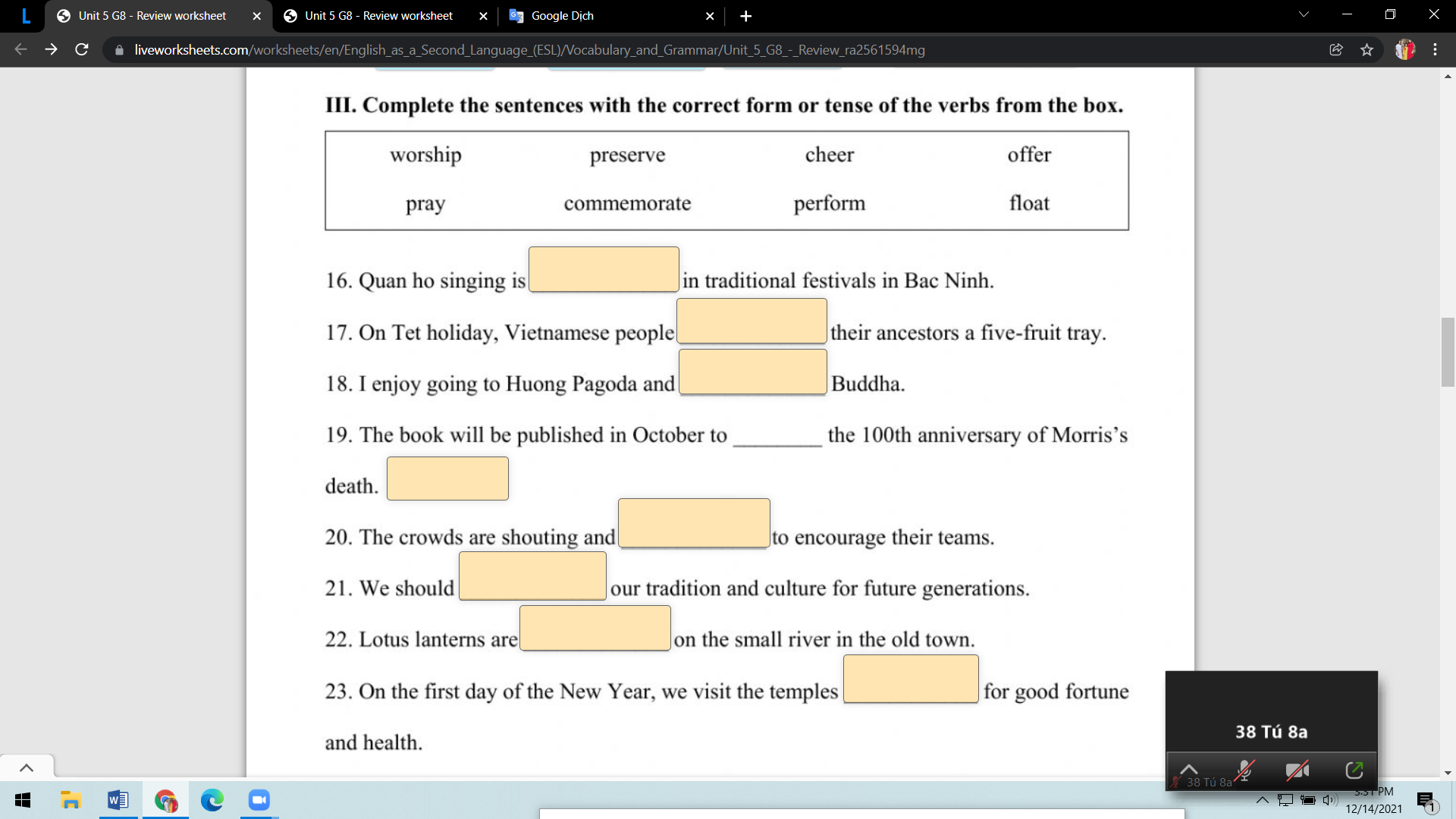 giúp mk vs ạ mk cần gấp ạ
giúp mk vs ạ mk cần gấp ạ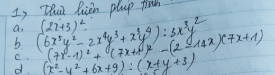
Câu 16:
a: Xét tứ giác MDHE có
\(\widehat{MDH}=\widehat{MEH}=\widehat{EMD}=90^0\)
=>MDHE là hình chữ nhật
b: Ta có: MDHE là hình chữ nhật
=>MH cắt DE tại trung điểm của mỗi đường và MH=DE
=>O là trung điểm chung của MH và DE
Ta có: MH=DE
mà DE=6cm
nên MH=6cm
Ta có: ΔHMP vuông tại H
=>\(HM^2+HP^2=MP^2\)
=>\(MP^2=6^2+8^2=100\)
=>\(MP=\sqrt{100}=10\left(cm\right)\)
Xét ΔHMP có
O,A lần lượt là trung điểm của HM,HP
=>OA là đường trung bình của ΔHMP
=>OA//MP và \(OA=\dfrac{MP}{2}=5\left(cm\right)\)
c: MDHE là hình chữ nhật
=>\(\widehat{DEH}=\widehat{DMH}\)
mà \(\widehat{DMH}=\widehat{P}\left(=90^0-\widehat{N}\right)\)
nên \(\widehat{DEH}=\widehat{P}\)
Ta có: ΔPEH vuông tại E
mà EA là đường trung tuyến
nên AE=AH
=>\(\widehat{AEH}=\widehat{AHE}\)
Ta có: \(\widehat{AED}=\widehat{AEH}+\widehat{DEH}\)
\(=\widehat{AHE}+\widehat{P}=90^0\)
=>ΔAED vuông tại E
cậu vẽ hình nx đk ko