cho a=4+4 mũ 2 +4 mũ 3 + ....+4 mũ 23 +4 mũ 24.chứng minh a chia hết cho 20:21:420
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = 4 + 4² + 4³ + ... + 4²³ + 4²⁴
Số số hạng của A:
24 - 1 + 1 = 24
Do 24 ⋮ 2 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 2 số hạng như sau:
A = (4 + 4²) + (4³ + 4⁴) + ... + (4²³ + 4²⁴)
= 20 + 4².(4 + 4²) + ... + 4²².(4 + 4²)
= 20 + 4².20 + ... + 4²².20
= 20.(1 + 4² + ... + 4²²) ⋮ 20
Vậy A⋮ 20 (1)
Do 24 ⋮ 3 nên ta có thể nhóm các số hạng của A thành từng nhóm mà mỗi nhóm có 3 số hạng như sau:
A = (4 + 4² + 4³) + (4⁴ + 4⁵ + 4⁶) + ... + (4²² + 4²³ + 4²⁴)
= 4.(1 + 4 + 4²) + 4⁴.(1 + 4 + 4²) + ... + 4²².(1 + 4 + 4²)
= 4.21 + 4⁴.21 + ... + 4²².21
= 21.(4 + 4⁴ + ... + 4²²) ⋮ 21
Vậy A ⋮ 21 (2)
Từ (1) và (2) ⇒ A ⋮ 20 . 21 (do 20 và 21 nguyên tố cùng nhau)
⇒ A ⋮ 420
Vậy A chia hết cho 20; 21; 420

Có. T= 41+42+.......+423+424
41T=42+43+........+424+425
Ta lấy 41T-T, ta được:
41T-T=425-41
3T=425-41
T=(425-41):3
Vậy T chia hết cho 3
nhớ k nhé
41+42+...+423+424 chia hết cho 21 => 41+42+...+423+424 chia hết cho 3

số mũ của dãy cộng :
( 24 - 1 ) : 1 + 1 = 24 ( mũ )
tổng các mũ :
( 24 + 1 ) x 24 : 2 = 300
A = 3300
vậy thì a có chia hết cho 120 không .
câu trả lời theo mình là không
nhé !
mong các bạn giúp đỡ trong thời gian tới

A=1+4+4^2+...+4^59A=1+4+4^2+...+4^59
A=(1+4)+(4^2+4^3)+...+(4^58+4^59)A=(1+4)+(4^2+4^3)+...+(4^58+4^59)
A=(1+4)+4^2(1+4)+...+4^58(1+4)A=(1+4)+4^2(1+4)+...+4^58(1+4)
A=5+4^2.5+...+4^58.5A=5+4^2.5+...+4^58.5
A=5(1+4^2+...+4^48)A=5(1+4^2+...+4^58)
A=5(1+4^2+...+4^58) chia hết cho 5
vậy A chia hết cho 5
A=1+4+4^2+...+4^59A=1+4+4^2+...+4^59
A=(1+4+4^2)+(4^3+4^4+4^5)+...+(4^57+4^58+4^59)A=(1+4+4^2)+(4^3+4^4+4^5)+...+(4^57+4^58+4^59)
A=(1+4+4^2)+4^3(1+4+4^2)+...+4^57(1+4+4^2)A=(1+4+4^2)+4^3(1+4+4^2)+...+4^57(1+4+4^2)
A=21+4^3.21+...+4^57.21A=21+4^3.21+...+4^57.21
A=21(1+4^3+...+4^57)A=21(1+4^3+...+4^57)
A=21(1+4^3+...+4^57) chia hết cho 21
vậy A chia hết cho 21
mik làm xong rồi nhớ k cho mik nha mik cảm ơn

*Ta có: A\(=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(=\left(2+2^2\right)+2^2\times\left(2+2^2\right)+...+2^{2008}\times\left(2+2^2\right)\)
\(=\left(2+2^2\right)\times\left(1+2^2+2^3+...+2^{2008}\right)\)
\(=6\times\left(2^2+2^3+...+2^{2008}\right)\)
\(=3\times2\times\left(2^2+2^3+...+2^{2008}\right)\)
\(\Rightarrow A⋮3\)
*Ta có: A \(=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(=2\times\left(1+2+2^2\right)+2^4\times\left(1+2+2^2\right)+...+2^{2008}\times\left(1+2+2^2\right)\)
\(=\left(1+2+2^2\right)\times\left(2+2^4+2^7+...+2^{2008}\right)\)
\(=7\times\left(2+2^4+2^7+...+2^{2008}\right)\)
\(\Rightarrow A⋮7\)
Mình sửa lại đề C 1 chút xíu
*Ta có: C \(=3^1+3^2+3^3+3^4+...+3^{2010}\)
\(=\left(3+3^2\right)+3^2\times\left(3+3^2\right)+...+3^{2008}\times\left(3+3^2\right)\)
\(=\left(3+3^2\right)\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(=12\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(=4\times3\times\left(1+3^2+3^3+...+3^{2008}\right)\)
\(\Rightarrow C⋮4\)
Các câu khác làm tương tự nhé. Chúc bạn học tốt!

a) \(A=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(A=\left(2^1+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\)
\(A=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{2009}\left(1+2\right)\)
\(A=3\left(2+2^3+...+2^{2009}\right)⋮3\)
\(A=2^1+2^2+2^3+2^4+...+2^{2010}\)
\(A=\left(2^1+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\)
\(A=2\left(1+2+2^2\right)+2^4\left(1+2+2^2\right)+...+2^{2008}\left(1+2+2^2\right)\)
\(A=7\left(2^1+2^4+...+2^{2008}\right)⋮7\)
Các ý dưới bạn làm tương tự nhé.
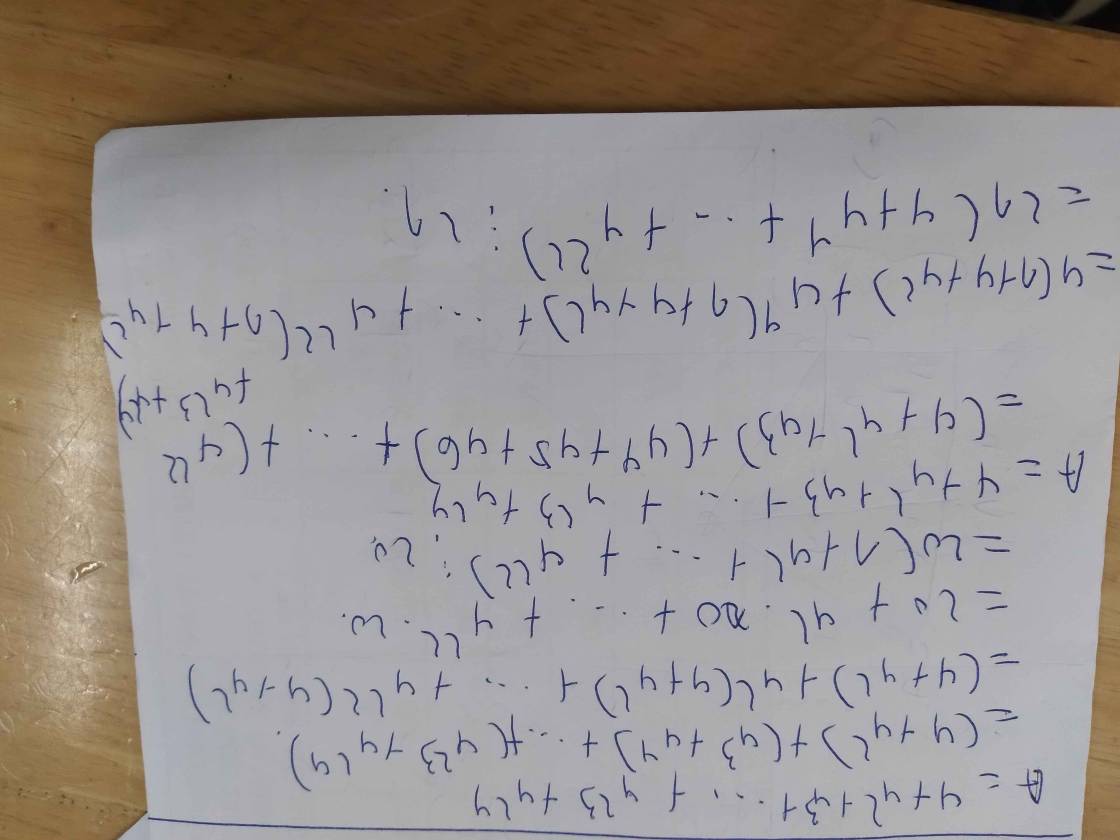
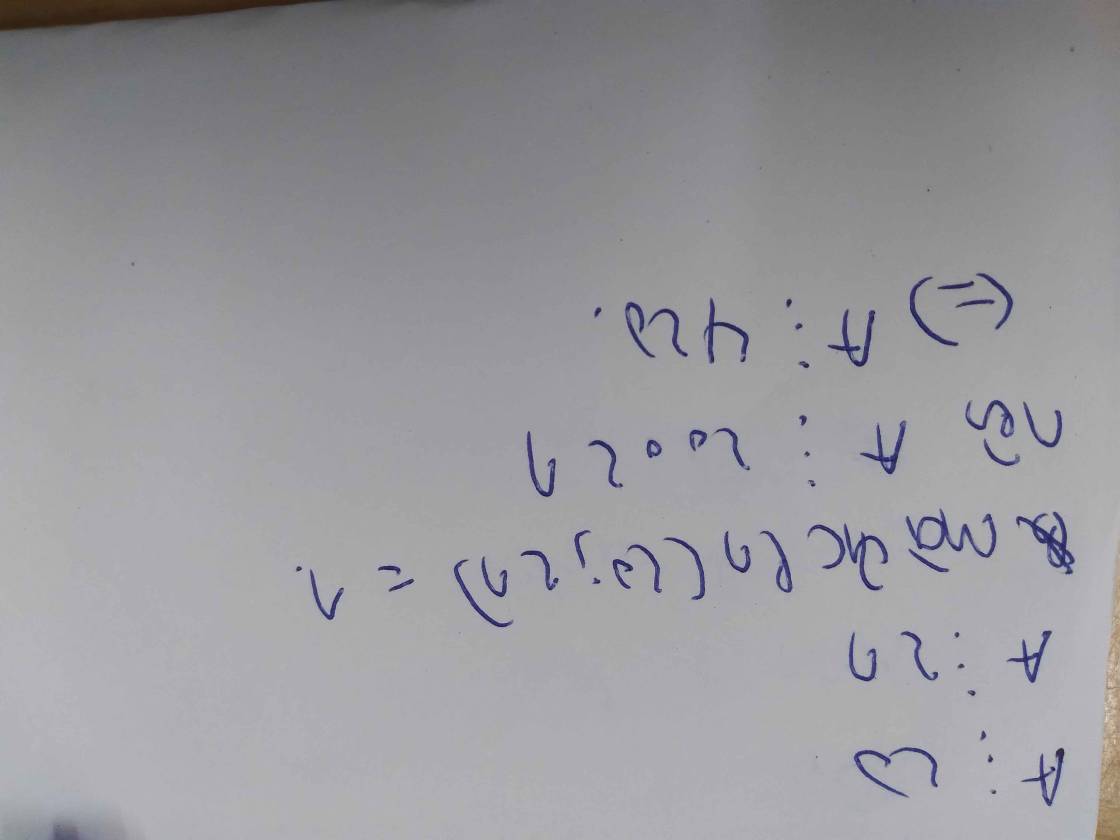
A = 4 + 42 + 43 +...+ 423 +424
Xét dãy số: 1;2;3;..; 24 dãy số này có 24 số hạng vì
24 : 2 = 12
Vậy nhóm hai số hạng liên tiếp của A vào nhau ta có:
A = (4 + 42) + (43 + 44) + ... + (423 + 424)
A = (4 + 16) + 42.(4 + 42) + .... + 422.(4 + 42)
A = 20 + 42.20 + ... + 422.20
A = 20.( 1 + 42 + ... + 422)
20 ⋮ 20 ⇒ A = 20.(1 + 42 + ... + 422) ⋮ 20 (đpcm)
A = 4 + 42 + 43 + ... + 423 + 424
Dãy số trên có 24 số hạng vì 24 : 3 = 8
Vậy ta nhóm 3 số hạng liên tiếp của A thành nhóm thì
A = (4 + 42 + 43) + (44 + 45 + 46) + ... + (422 + 423 + 424)
A = 4.(1 + 4 + 42) + 44.(1 + 4 + 42) + ... + 422.(1 + 4 + 42)
A = 4.21 + 44.21 + ... + 422.21
A =21.(4 + 44 + ... + 422)
Vì 21 ⋮ 21 vậy A = 21.(4 + 44 + ... + 422) ⋮ 21