23x + 14y - 8 x+ y bt x+y=100
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án B.
Hoành độ giao điểm của hai đường cong đã cho là nghiệm của phương trình
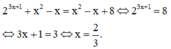

Ta có:
\(x-3y-2+\sqrt{y\left(x-y-1\right)+x}=0\Leftrightarrow\left(x-y\right)-2\left(y+1\right)+\sqrt{\left(x-y\right)\left(y+1\right)}=0\)
Xét y=-1 thay vào tìm x
Xét y khác -1
\(pt\Leftrightarrow\frac{x-y}{y+1}-2+\sqrt{\frac{x-y}{y+1}}=0\) (2)
Đặt \(\sqrt{\frac{x-y}{y+1}}=a\left(a\ge0\right)\)
pt(2) trở thành
\(a^2+a-2=0\Leftrightarrow\left(a-1\right)\left(a+2\right)=0\)
Làm r nhưng mà làm lại hjhjhj
\(\hept{\begin{cases}x-3y-2+\sqrt{y\left(x-y-1\right)+x}=0\left(1\right)\\3\sqrt{8-x}-\frac{4y}{\sqrt{y+1}+1}=x^2-14y-8\left(2\right)\end{cases}}\)
\(ĐK:\hept{\begin{cases}y\left(x-y-1\right)+x\ge0\\x\le8\\y\ge-1\end{cases}}\)
\(\left(1\right)\Leftrightarrow\sqrt{y\left(x-y-1\right)+x}=-\left(x-3y-2\right)\)\(\Leftrightarrow\sqrt{xy-y^2-y+x}=-\left(x-3y-2\right)\)
\(\Leftrightarrow-\sqrt{\left(x-y\right)\left(y+1\right)}=x-3y-2\)\(\Leftrightarrow-\sqrt{\left(x-y\right)\left(y+1\right)}=\left(x-y\right)-2\left(y+1\right)\)
\(\Leftrightarrow\left(x-y\right)-2\left(y+1\right)+\sqrt{\left(x-y\right)\left(y+1\right)}=0\)(*)
* Với y = -1 thì từ (*) suy ra x = -1
Thay nghiệm \(\left(x,y\right)=\left(-1,-1\right)\)vào (2) thì ta thấy không đúng
* Với \(y\ne-1\)thì chia hai vế của phương trình (*) cho y + 1, ta được: \(\left(\frac{x-y}{y+1}\right)-2+\sqrt{\frac{x-y}{y+1}}=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{\frac{x-y}{y+1}}=1\left(tm\right)\\\sqrt{\frac{x-y}{y+1}}=-2\left(ktm\right)\end{cases}}\Leftrightarrow x-y=y+1\Leftrightarrow y=\frac{x-1}{2}\)
Khi đó \(\left(2\right)\Leftrightarrow3\sqrt{8-x}-\frac{4.\frac{x-1}{2}}{\sqrt{\frac{x-1}{2}+1}+1}=x^2-14.\frac{x-1}{2}-8\)
\(\Leftrightarrow3\sqrt{8-x}-\frac{2\left(x-1\right)}{\sqrt{\frac{x-1}{2}+1}+1}-x^2+7x+1=0\)
Đặt \(f\left(x\right)=3\sqrt{8-x}-\frac{2\left(x-1\right)}{\sqrt{\frac{x-1}{2}+1}+1}-x^2+7x+1\)
Ta có: \(f\left(-1\right)=6;f\left(8\right)=-3-6\sqrt{2}\Rightarrow f\left(-1\right).f\left(8\right)=-18-36\sqrt{2}< 0\)
\(\Rightarrow f\left(x\right)\)có ít nhất một nghiệm trên đoạn \(\left[-1;8\right]\)
Lại có f(7) = 0 \(\Rightarrow\)x = 7 là nghiệm của f(x) \(\Rightarrow y=3\)
Vậy hệ phương trình có 1 nghiệm \(\left(x,y\right)=\left(7,3\right)\)

Bài 2:
1) \(7x^2+2x=0\)
\(\Leftrightarrow x\left(7x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\7x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{2}{7}\end{matrix}\right.\)
2) \(2x\left(x-9\right)+5\left(x-9\right)=0\)
\(\Leftrightarrow\left(x-9\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-9=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=9\\x=-\dfrac{5}{2}\end{matrix}\right.\)
3) \(x^2+8x+16=0\)
\(\Leftrightarrow\left(x+4\right)^2=0\)
\(\Leftrightarrow x+4=0\)
\(\Leftrightarrow x=-4\)
Bài 1:
2) \(24x-18y+30=6\left(4x-3y+5\right)\)
5) \(x^2+14x+49=\left(x+7\right)^2\)
6) \(27x^3+y^3=\left(3x+y\right)\left(9x^2-3xy+y^2\right)\)

\(x^3+8y^3\\ =x^3+\left(2y\right)^3\\ =\left(x+2y\right)\left(x^2-2xy+4y^2\right)\)
\(8y^3-125\\ =\left(2y\right)^3-5^3\\ =\left(2y-5\right)\left(4y^2+10y+25\right)\)
\(a^6-b^3\\ =\left(a^2\right)^3-b^3\\ =\left(a^2-b\right)\left(a^4+a^2b+b^2\right)\)
\(8x^3-\frac{1}{8}\\ =\left(2x\right)^3-\left(\frac{1}{2}\right)^3\\ =\left(2x-\frac{1}{2}\right)\left(4x^2+x+\frac{1}{4}\right)\)
\(x^{32}-1\\ =\left(x^{16}\right)^2-1^2\\ =\left(x^{16}-1\right)\left(x^{16}+1\right)\\ =\left(x^8-1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^4-1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x^2-1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\left(x^8+1\right)\left(x^{16}+1\right)\)
\(4x^2+4x+1\\ =\left(2x+1\right)^2\)
\(x^2-20x+100\\ =\left(x-10\right)^2\)
\(y^4-14y^2+49\\ =\left(y^2-7\right)^2\)

Vì 35x=14y=10z
=> \(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{7}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có :
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{\left(x+z-y\right)}{2+5-7}=\dfrac{20}{0}=0\)
Có : x/2 = 0 => x = 2*0 = 0
y/5 = 0 => y = 5*0 = 0
z/7 = 0 => z=7*0=0
Vậy, ..

a) Thay \(x=0,25y\) vào M ta có:
\(M=26\cdot\left(0,25y\right)^2+y\left(2\cdot0,25y+y\right)-10\cdot0,25y\cdot\left(0,25y+y\right)\)
\(M=1,625y^2+y\cdot1,5y-2,5y\cdot1,25y\)
\(M=1,625y^2+1,5y^2-3,125y^2\)
\(M=0\)
b) Thay \(x+6y=9\Rightarrow x=9-6y\) vào N ta có:
\(N=50y^2+\left(9-6y\right)\left(9-6y-2y\right)+14y\left(9-6y-y\right)\)
\(N=50y^2+\left(9-6y\right)\left(9-8y\right)+14\left(9-7y\right)\)
\(N=50y^2+81-72y-54y+48y^2+126-98y\)
\(N=2y^2-224y+207\)
\(a,M=26x^2+y\left(2x+y\right)-10x\left(x+y\right)\\ =26x^2+2xy+y^2-10x^2-10xy\\ =16x^2-8xy+y^2\\ =16\left(x^2-\dfrac{1}{2}xy+\dfrac{1}{16}y^2\right)\\ =16\left(x^2-2.x.y.\dfrac{1}{4}+\dfrac{1}{16}y^2\right)=16\left(x-\dfrac{1}{4}y\right)^2\\ Vì:x=0,25y\Rightarrow y=4x\\ Vậy:M=16\left(x-\dfrac{1}{4}y\right)^2=16\left(x-x\right)^2=16.0^2=0\\ Vậy:tại.x=0,25y.thìM=0\)
23x+14y-8x+y
=(23x-8x)+(14y+y)
=15x+15y
=15(x+y)
\(=15\cdot100=1500\)