Tìm chữ số a,b để 5a34b chia cho 5 dư 3 và chia hết cho 9.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5a34b chia hết cho 9 thì tổng của các chữ số của nó phải chia hết cho 9.
Ta có:
5+a+3+4+b=12
Cần phải thêm 6 đơn vị nữa thì mới chia hết cho 9.
Nhưng muốn chia 5 dư 3 thì b khác 5 và 0
Vậy B=3.
Vậy A=6-3=3
Đáp số:A=3 B=3
\(\overline{5a34b}\)chia cho \(5\)dư \(3\)nên chữ số tận cùng của \(\overline{5a34b}\)chia cho \(5\)dư \(3\)nên \(b=3\)hoặc \(b=8\).
Với \(b=3\): \(\overline{5a343}\)chia hết cho \(9\)nên \(5+a+3+4+3=15+a\)chia hết cho \(9\)
suy ra \(a=3\).
Với \(b=8\): \(\overline{5a348}\)chia hết cho \(9\)nên \(5+a+3+4+8=20+a\)chia hết cho \(9\)
suy ra \(a=7\).

Chia cho 5 dư 3 thì có tận cùng là 3 hoặc 8 => b=3 hoặc b=8
Chi hết cho 9 thì tổng các chữ số chia hết cho 9 => 5+a+3+4+b=12+a+b chia hết cho 9.
Với b=3 ta có: 12+a+3 chia hết cho 9 => 15+a chia hết cho 9 => a=3
Với b=8 ta có: 12+a+8 chia hết cho 9 => 20+a chia hết cho 9 => a=7
Vậy a=3 ; b=3 hoặc a=7 ; b=8

Theo đề bài ta có :
5a34b chia hết cho 5; 2 và 9
+ Vì số chia hết cho 2 và 5 là số có chữ số tận cùng là 0 nên b = 0
+ Ta có : 5 + 3 + 4 + 0 = 12. Mà số chia hết cho 9 là số có tổng các chữ số chia hết cho 9 nên a có thể bằng 6
Vậy a = 6; b = 0

Chia hết cho 5 tận cùng là 0, 5
Chia hết cho 2 tận cùng : 0, 2, 4, 6, 8
Chia hết cho 9 là tổng các chưa số chia hết cho 9
=>Số cần tìm 56340
để 5a34b chia hết cho cả 2 và 5 suy ra b=o
ta có 5a340 :5+a+3+4+0=12+a
để 5a340chia hết cho 9 thì 12+a phải chia hết cho 9
suy ra a=6

bài 2:
vì 4a12b chia hết cho cả 2 và 5 nên b=0
để 4a120 chia hết cho 9 thì 4+a+1+2+0 phải chia hết cho 9 => a=2
bài 1:
a/ ta có : 18 = 2x9 => a là số chẵn và 7+3+a chia hết cho 9 => a=8
vậy a=8
b/ để 792a chia hết cho 3 và 5 => a=0 hoặc 5 và 7+9+2+a chia hết cho 3 => a=0
c/ để 87a chia hết cho 5 và 9 => a=0 hoặc a=5 và 8+7+a chia hết cho 9 => ko tìm được a thoả mãn
d/ a=5 và a=8

Bài 1 :
a)
Ta có: 87ab ⋮ 9 ⇔ (8 + 7 + a + b) ⁝⋮ 9 ⇔ (15 + a + b) ⋮ 9
Suy ra: (a + b) ∈ {3; 12}
Vì a – b = 4 nên a + b > 3. Suy ra a + b = 12
Thay a = 4 + b vào a + b = 12, ta có:
b + (4 + b) = 12 ⇔ 2b = 12 – 4
⇔ 2b = 8 ⇔ b = 4
a = 4 + b = 4 + 4 = 8
Vậy ta có số: 8784.
b)
⇒ (7+a+5+b+1) chia hết cho 3
⇔ (13+a+b) chia hết cho 3
+ Vì a, b là chữ số, mà a-b=4
⇒ a,b ∈ (9;5) (8;4) (7;3) (6;2) (5;1) (4;0).
Thay vào biểu thức 7a5b1, ta được :
ĐA 1: a=9; b=5.
ĐA 2: a=6; b=2.
Bài 2 :
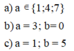

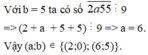

Chia cho 5 dư 3 thì có tận cùng là 3 hoặc 8 => b=3 hoặc b=8
Chi hết cho 9 thì tổng các chữ số chia hết cho 9 => 5+a+3+4+b=12+a+b chia hết cho 9.
Với b=3 ta có: 12+a+3 chia hết cho 9 => 15+a chia hết cho 9 => a=3
Với b=8 ta có: 12+a+8 chia hết cho 9 => 20+a chia hết cho 9 => a=7
Vậy a=3 ; b=3 hoặc a=7 ; b=8
5a34b chia 5 dư 3 => b là 3 hoặc 8
(+) b = 3
=> 5a343 phải chia hết cho 9
5 + a + 3 + 4 + 3 = 15 + a chia hết cho 9 => a = 3
(+) b = 8
=> 5a348 chia hết cho 9 => 5 + a + 3 + 4 + 8 chia hết cho 9 => 20 + a chia hết cho 9 => a =7
Vậy ta có hai sô 53343 và 57348