Tính E1+E2⋮2 với:
E1=6+15+24+...+456 và E2=120+135+150+...+255.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án: A
q1 và q2 trái dấu, để E 2 = 16 E 1 thì M phải nằm trong đoạn AB
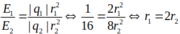
và r1 + r2 = 12 => r1 = 8cm

Đáp án A
Xét hệ:

Đường tròn ngoại tiếp hình chữ nhật ABCD có tâm O và bán kính

Vậy phương trình đường tròn cần tìm là:


Chọn đáp án C.
Giả sử ở thời điểm t nào đó ta có như trên VTLG
Giả sử suất điện động xuất hiện trong khung dây có dạng e 1 = E 0 cos ω t 1 e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 (1)
e 2 = E 0 cos ω t + 2 π 3 e 3 = E 0 cos ω t − 2 π 3 → e 2 - e 1 = ± 30 E 0 cos ω t + 2 π 3 − cos ω t − 2 π 3 = ± 30 ( 2 )
Áp dụng công thức toán học cos a − cos b = − 2 sin a + b 2 sin a − b 2
Phương trình (2) được viết lại: − 2 E 0 sin ω t sin 2 π 3 = ± 30 . Kết hợp với (1) ta có:
− 2 E 0 sin ω t sin 2 π 3 = ± 30 e 1 = E 0 cos ω t = 30 ⇔ E 0 sin ω t = ± 10 3 E 0 cos ω t = 30 ⇒ E 0 ± 10 3 2 + E 0 30 2 = 1 ⇒ E 0 = 20 3 ≈ 34 , 6 V
Lời giải:
$E_1$ là tổng của các số cách đều nhau 9 đơn vị
Số số hạng của $E_1$: $(456-6):9+1=51$
$E_1=(456+6).51:2=11781$
$E_2$ là tổng của các số cách đều nhau 15 đơn vị
Số số hạng của $E_2$ là: $(255-120):15+1=10$
$E_2=(255+120).10:2=1875$
$(E_1+E_2):2=(11781+1875):2=6828$