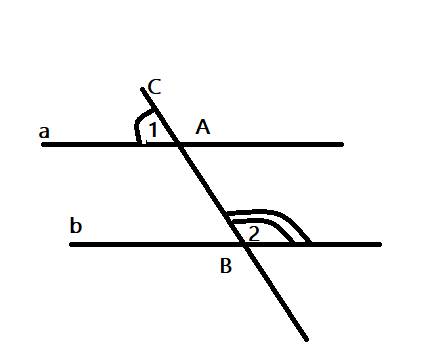
Cho hình vẽ, biết A1 =80 độ, B3 = 100 độ. Hãy giải thích tại sao a//b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(B_1=A_1=70^o\)
\(\Rightarrow a//b\) (\(A_1\&B_1\)ở vị trí so le trong)
b) \(A_3=A_1=70^o\) (đối đỉnh)
\(A_4=180-A_1=180-70=110^o\) (góc kề bù)
Tương tự B3; B4...

Do a // b nên ta có:
\(\widehat{A_1}=\widehat{A_3}=54^0(đối đỉnh)\)
\(\widehat{A_3}+\widehat{A_2}=180^0\)
\(\Rightarrow\)\(\widehat{A_2}=180^0-54^0=126^0\)
a)\(\widehat{B_2}=\widehat{A_3}=54^0(đồng vị)\)
b)\(\widehat{A_2}=\widehat{A_4}=126^0(đối đỉnh)\)
\(\Rightarrow\)\(\widehat{A_4}=\widehat{B_3}=126^0(đồng vị)\)
\(\widehat{A_1}<\widehat{B_3}(54^0<126^0)\)
c)\(\widehat{A_4}+\widehat{B_2}=126^0+54^0=180^0\)

a:
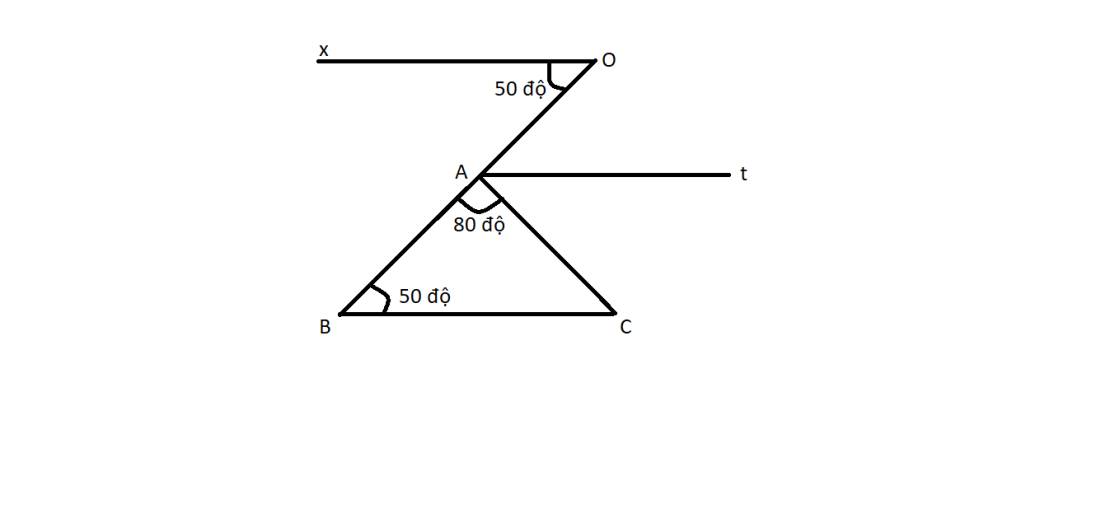
Xét ΔABC có góc OAC là góc ngoài tại đỉnh A
nên \(\widehat{OAC}+\widehat{BAC}=180^0\)
=>\(\widehat{OAC}=180^0-80^0=100^0\)
At là phân giác của góc OAC
=>\(\widehat{tAO}=\widehat{tAC}=\dfrac{\widehat{OAC}}{2}=\dfrac{100^0}{2}=50^0\)
\(\widehat{tAO}=\widehat{CBA}\)(=50 độ)
mà hai góc này là hai góc ở vị trí đồng vị
nên At//BC
\(\widehat{xOA}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Ox//BC
b:
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+80^0+50^0=180^0\)
=>\(\widehat{ACB}=50^0\)

a b c 1 2 3 4 1 2 3 4 A B
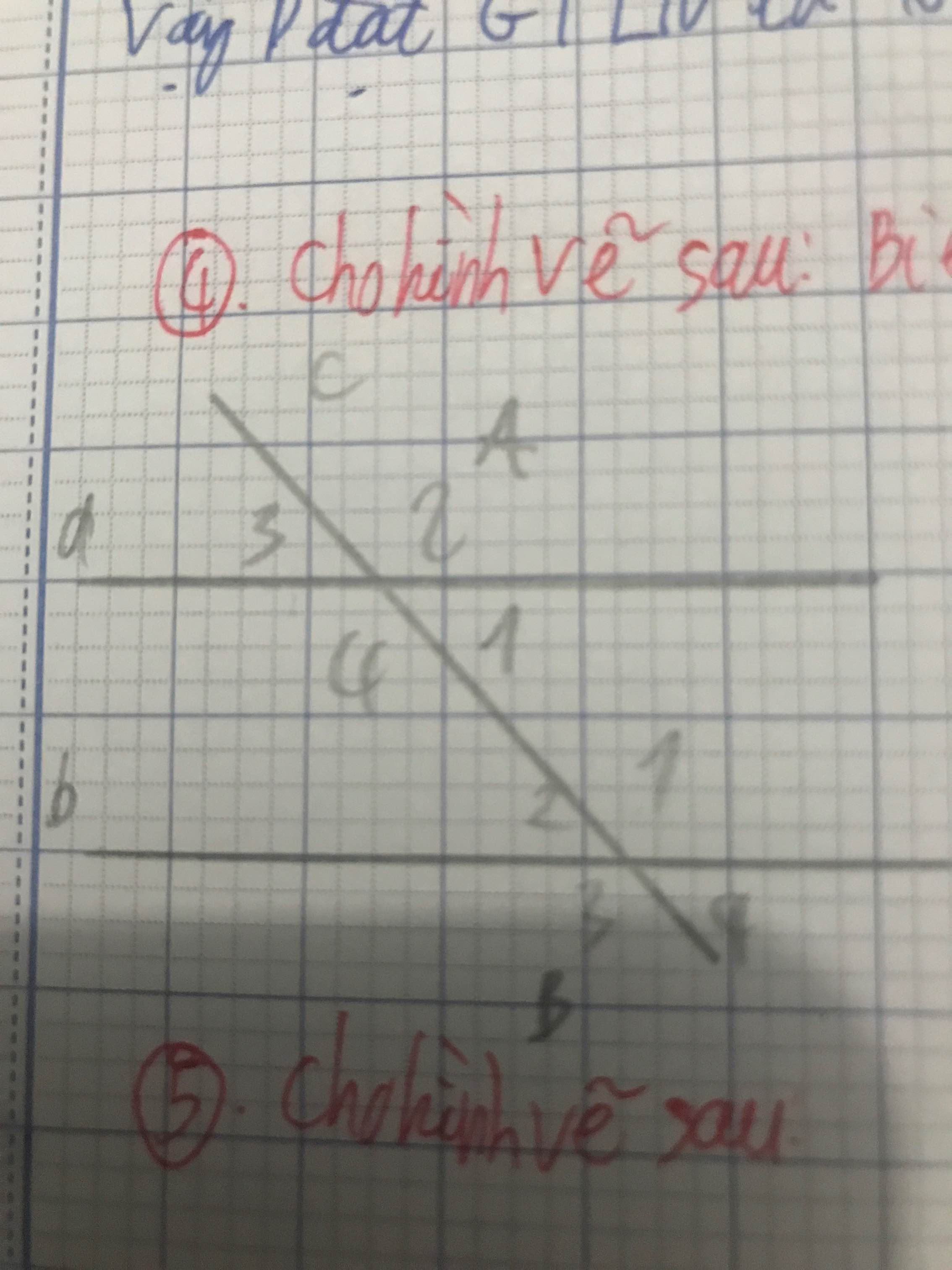
A1=55o (đồng vị); A2=180o-55o=125o (kề bù với A1); A3=55o (đối đỉnh với A1); A4=125o (đối đỉnh với A2);
B2=125o (đồng vị với A2); B3=55o (đối đỉnh với B1); B4=125o (đối đỉnh với B2)

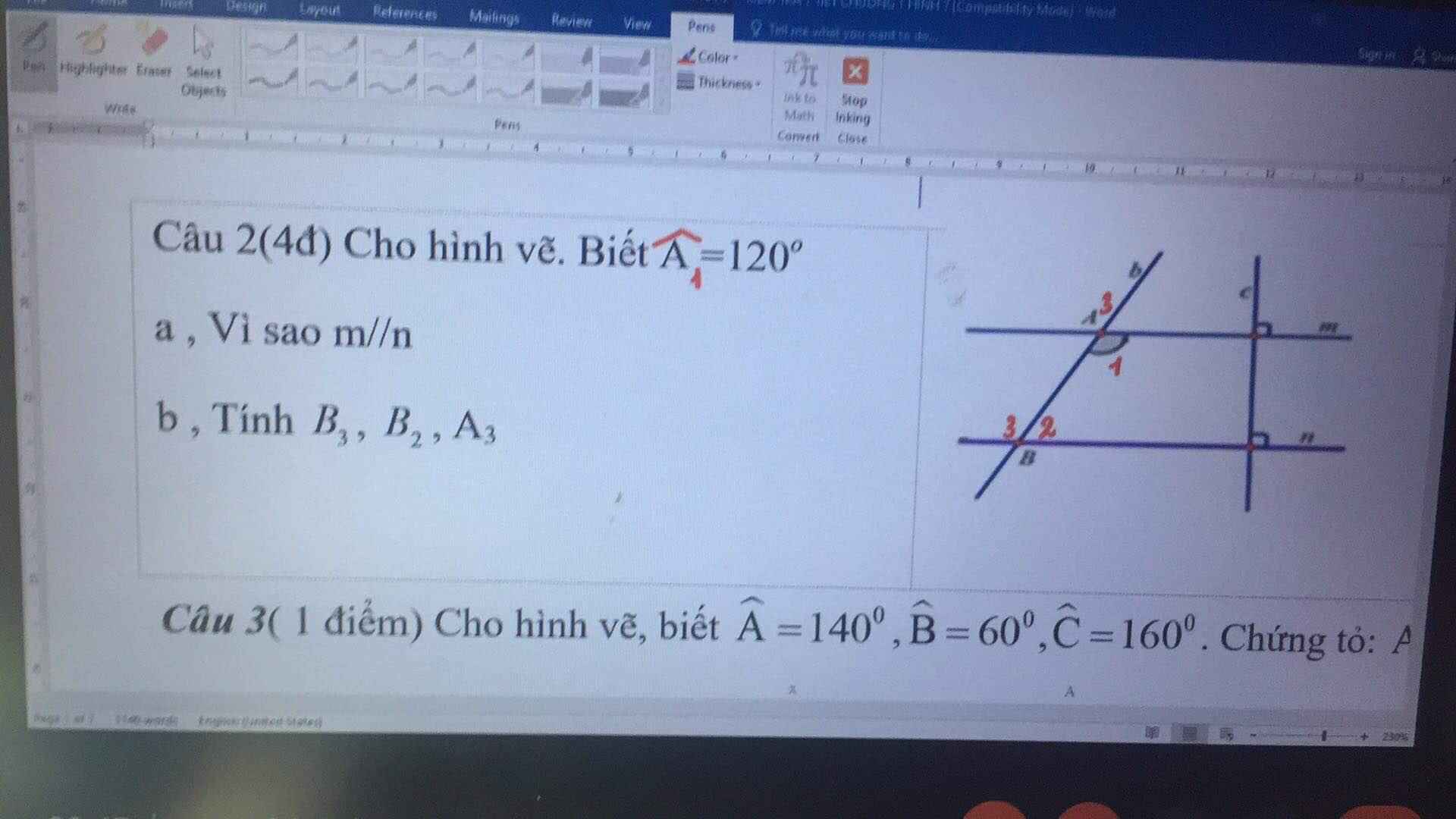
1.Ta có :
\(\left\{{}\begin{matrix}m\perp c\\n\perp c\end{matrix}\right.\Rightarrow m//n\)
2. \(\widehat{A_1}=\widehat{A_3}=120^o\)(2 góc đối đỉnh)
Do m // n
\(\Rightarrow\widehat{A_3}=\widehat{B_3}=120^o\)(2 góc đồng vị)
\(\widehat{B_2}+\widehat{B_3}=180^o\)(2 góc kề bù)
\(\Rightarrow\widehat{B_2}+120^o=180^o\\ \Rightarrow\widehat{B_2}=60^o\)

Bạn cho mình xin hình vẽ nha bạn
Hình vẽ đc chưa bạn