Chứng minh vectoAB + vectoCD=vectoAD - vectoBC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: vecto AB-vecto AD
=vecto DA+vecto AB
=vecto DB
-vecto CD-veco BC
=vecto CB-vecto CD
=vecto DC+vecto CB=vecto DB
=>vecto AB+vecto CD=vecto AD-vecto BC
b: \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CB}\)
\(\overrightarrow{CD}-\overrightarrow{BD}=\overrightarrow{CD}+\overrightarrow{DB}=\overrightarrow{CB}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CD}-\overrightarrow{BD}\)
=>\(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\)
c: \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}\)
\(\overrightarrow{CB}-\overrightarrow{CD}=\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)
=>\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)

A B C D
ta có \(\overrightarrow{BC}\cdot\left(2\overrightarrow{\cdot AD}-\overrightarrow{AB}\right)=2\cdot\overrightarrow{BC}\cdot\overrightarrow{AD}-\overrightarrow{BC}\cdot\overrightarrow{AB}=2a^2\)
(Do BC và AD cùng hướng, BC và AB vuông góc với nhau)

+) vecto AC + vecto BD = vecto AD + vecto DC + vecto BC + vecto CD
= vecto AD + vecto BC (1)
+) vecto MN = \(\frac{1}{2}\left(\overrightarrow{MD}+\overrightarrow{MC}\right)\)
\(\Leftrightarrow2\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{BC} \)\(=\overrightarrow{AD}+\overrightarrow{BC}\)\(\left(2\right)\)
Từ (1),(2) => đpcm

a) I là trung điểm
nên vectoAB+ vectoAC= 2AI (1)
vectoAD+ vectoAE=2AI (2)
Từ (1) và (2) suy ra câu a
b) vecto AB+ vectoAC= 2AI(cmt
vectoAD+ vectoAE= 2AI(cmt
vectoAS=vectoAB+ vectoAD+ vectoAC+ vectoAE
tương đương: vectoAS=(vectoAB+ vectoAC)+ (vectoAD+ vectoAE)
vectoAS=2AI+2AI= 4AI

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NB}+\overrightarrow{CM}+\overrightarrow{MN}+\overrightarrow{ND}\)
\(=\left(\overrightarrow{AM}+\overrightarrow{CM}\right)+\left(\overrightarrow{NB}+\overrightarrow{ND}\right)+2\overrightarrow{MN}\)
\(=\overrightarrow{0}+\overrightarrow{0}+2\overrightarrow{MN}=2\overrightarrow{MN}\)

a/ \(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}+\overrightarrow{DB}+\overrightarrow{BD}=\overrightarrow{AD}+\overrightarrow{CB}\)
b/ \(\overrightarrow{MN}+2\overrightarrow{PO}+\overrightarrow{MQ}=\overrightarrow{MN}+\overrightarrow{PM}+\overrightarrow{MQ}=\overrightarrow{MN}+\overrightarrow{PQ}=\overrightarrow{0}\)

\(\overrightarrow{AD}=\overrightarrow{BC}\) \(\Rightarrow\) ABCD là hình bình hành
Vậy D là đỉnh của hình bình hành ABCD
\(\overrightarrow{AE}=\overrightarrow{CA}\Rightarrow\overrightarrow{AE}-\overrightarrow{CA}=\overrightarrow{0}\Rightarrow\overrightarrow{AE}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow A\) là trung điểm CE hay E là điểm đối xứng C qua A

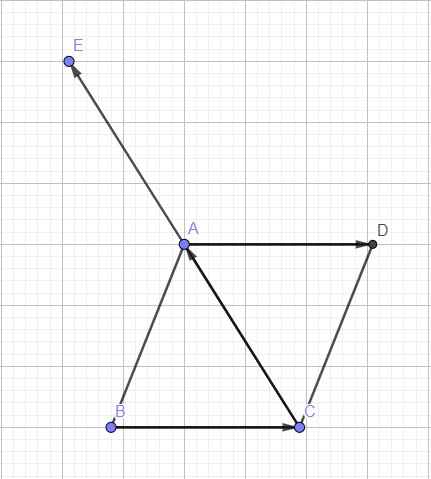
\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\)
\(\overrightarrow{AD}-\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}\)
Do đó: \(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AD}-\overrightarrow{CD}\)
=>\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}-\overrightarrow{BC}\)