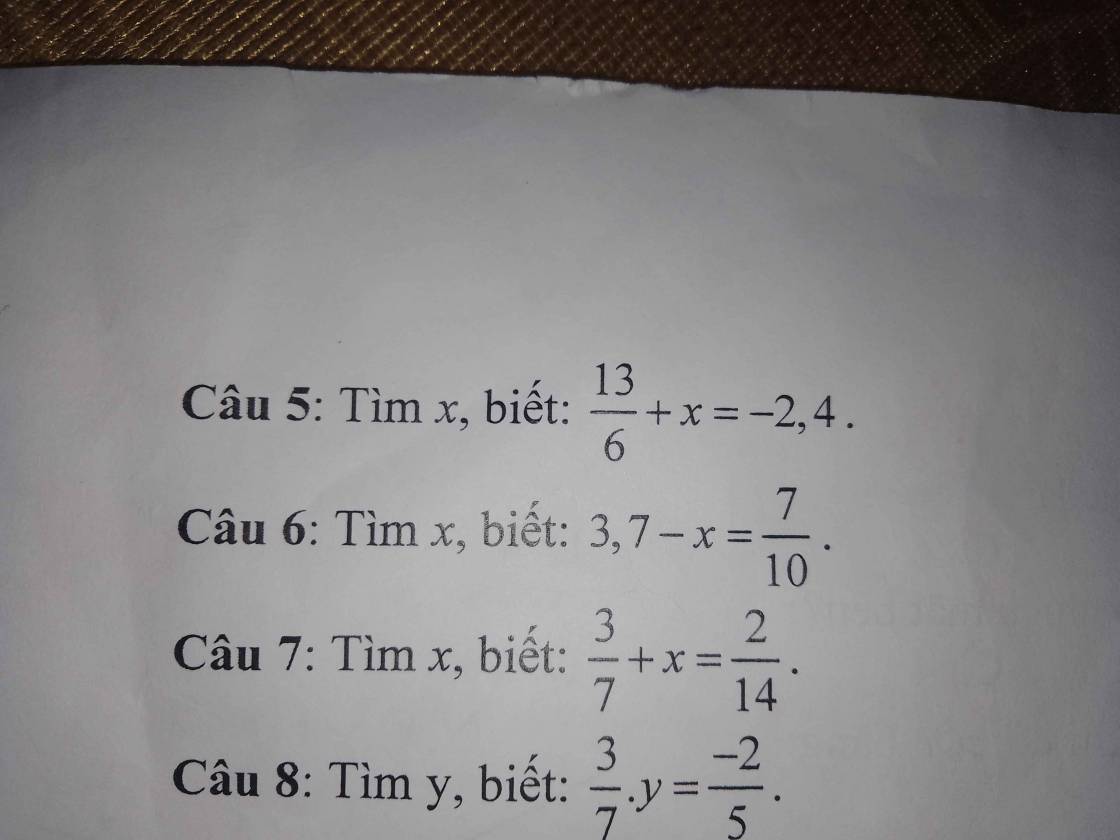 giải giúp ạ mik với ạ . em đang cần gấp.
giải giúp ạ mik với ạ . em đang cần gấp.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1) ĐKXĐ: \(x\ge0\)
2) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
3) ĐKXĐ: \(x\ge4\)
4) ĐKXĐ: \(x>16\)
5) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge0\end{matrix}\right.\)
6) ĐKXĐ: \(\left[{}\begin{matrix}x\le-1\\x\ge4\end{matrix}\right.\)
7) ĐKXĐ: \(\left[{}\begin{matrix}1\le x\\x< 3\end{matrix}\right.\)
8) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x>3\end{matrix}\right.\)
9) ĐKXĐ: \(x\in R\)
10) ĐKXĐ: \(x\in R\)
11) ĐKXĐ: \(x\in R\)
12) ĐKXĐ: \(x\in R\)
13) ĐKXĐ: \(x\in R\)
14) ĐKXĐ: \(x\in R\)
15) ĐKXĐ: \(x\in R\)
16) ĐKXĐ: \(x\ne-\dfrac{1}{2}\)
17) ĐKXĐ: \(x\ge7\)
18) ĐKXĐ: \(x\ge-5\)

\(1,\Leftrightarrow x^2-8x+16-x^2+x+12=7\\ \Leftrightarrow-7x=-21\\ \Leftrightarrow x=3\\ 2,\Leftrightarrow\left(x-4\right)^2-\left(x-4\right)=0\\ \Leftrightarrow\left(x-4\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=4\\x=5\end{matrix}\right.\)

a) \(\Leftrightarrow x^2+10x+25-x^2+8x-15=-8\\ \Leftrightarrow18x=-18\\ \Leftrightarrow x=-1\)
b) \(\Leftrightarrow\left(2x+1\right)^2-3\left(2x+1\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x+1-3\right)=0\\ \Leftrightarrow\left(2x+1\right)\left(2x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)

\(1,\\ a,\dfrac{8x}{2xy}=\dfrac{4x}{y}\\ b,\dfrac{2xy}{6y}=\dfrac{x}{3}\\ c,\dfrac{3\left(x+2\right)}{2x}=\dfrac{6\left(x+2\right)}{4x}\\ d,\dfrac{4\left(x-2\right)}{3\left(x+1\right)}=\dfrac{8\left(x-2\right)x}{6\left(x+1\right)x}\\ 2,\\ \dfrac{x^2+3x+2}{x^2+x}=\dfrac{x^2+x+2x+2}{x\left(x+1\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)}=\dfrac{x+2}{x}\\ 3,\\ \dfrac{x^2-3x}{x^2-9}=\dfrac{x}{x+3}\)

Bài 3:
Ta có: \(x^2-2x+4=\left(x-1\right)^2+3\ge3\forall x\)
\(\Leftrightarrow P=\dfrac{15}{x^2-2x+4}=\dfrac{15}{\left(x-1\right)^2+3}\le5\forall x\)
Dấu '=' xảy ra khi x=1

\(a^3+b^3+c^3=3abc\)
=>\(\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
=>\(\left(a+b+c\right)\left[\left(a+b\right)^2-c\left(a+b\right)+c^2\right]-3ab\left(a+b+c\right)=0\)
=>\(\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\)
=>\(a^2+b^2+c^2-ab-ac-bc=0\)
=>\(2a^2+2b^2+2c^2-2ab-2ac-2bc=0\)
=>\(\left(a^2-2ba+b^2\right)+\left(b^2-2cb+c^2\right)+\left(a^2-2ac+c^2\right)=0\)
=>\(\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2=0\)
=>\(\left\{{}\begin{matrix}a-b=0\\b-c=0\\a-c=0\end{matrix}\right.\Leftrightarrow a=b=c\)
\(A=\dfrac{a^{2023}}{b^{2023}}+\dfrac{b^{2023}}{c^{2023}}+\dfrac{c^{2023}}{a^{2023}}\)
\(=\dfrac{a^{2023}}{a^{2023}}+\dfrac{b^{2023}}{b^{2023}}+\dfrac{c^{2023}}{c^{2023}}\)
=1+1+1
=3

\(1,=3ab\left(1-2a+b\right)\\ 2,=\left(x-y\right)\left(x+y\right)-7\left(x+y\right)=\left(x+y\right)\left(x-y-7\right)\\ 3,=\left(a-5\right)\left(5a-2\right)\\ 4,=5x\left(x-3\right)-\left(x-3\right)\left(x+3\right)=\left(x-3\right)\left(4x-3\right)\\ 5,=9a^2-\left(b-2\right)^2=\left(3a-b+2\right)\left(3a+b-2\right)\\ 6,=2x^2-4x+3x-6=\left(x-2\right)\left(2x+3\right)\\ 7,=3x^2\left(2x-5\right)\\ 8,=\left(3x-5\right)\left(3x+5\right)\\ 9,=4x^2\left(x-y\right)-x\left(x-y\right)=x\left(4x-1\right)\left(x-y\right)\)



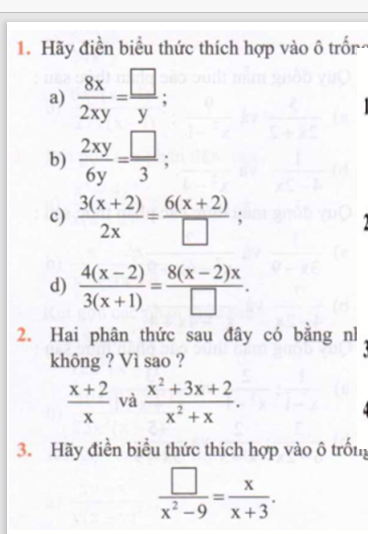 Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ Mọi người giải giúp em với ạ em đang cần gấp ạ
Mọi người giải giúp em với ạ em đang cần gấp ạ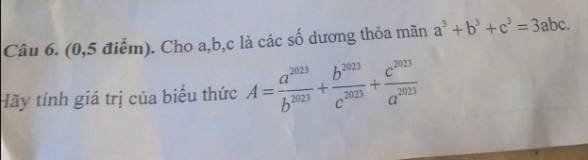
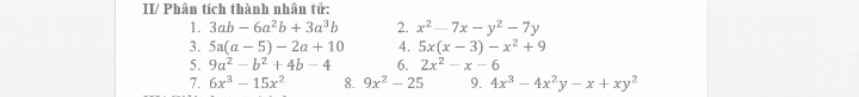
Câu 5:
\(\dfrac{13}{6}+x=-2,4\)
\(\Rightarrow\dfrac{13}{6}+x=-\dfrac{12}{5}\)
\(\Rightarrow x=-\dfrac{12}{5}-\dfrac{13}{6}\)
\(\Rightarrow x=-\dfrac{137}{30}\)
Câu 6:
\(3,7-x=\dfrac{7}{10}\)
\(\Rightarrow\dfrac{37}{10}-x=\dfrac{7}{10}\)
\(\Rightarrow x=\dfrac{37}{10}-\dfrac{7}{10}\)
\(\Rightarrow x=3\)
Câu 7:
\(\dfrac{3}{7}+x=\dfrac{2}{14}\)
\(\Rightarrow\dfrac{3}{7}+x=\dfrac{1}{7}\)
\(\Rightarrow x=\dfrac{1}{7}-\dfrac{3}{7}\)
\(\Rightarrow x=-\dfrac{2}{7}\)
Câu 8:
\(\dfrac{3}{7}\cdot y=\dfrac{-2}{5}\)
\(\Rightarrow y=\dfrac{-2}{5}:\dfrac{3}{7}\)
\(\Rightarrow y=\dfrac{-2}{5}\cdot\dfrac{7}{3}\)
\(\Rightarrow y=-\dfrac{14}{15}\)