giá trị lớn nhất của biểu thức 3 + 10x - x^2
đáp án thôi cg đc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NA
1
Những câu hỏi liên quan
MH
1
MH
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 10 2023
\(a,\\ A=25x^2-10x+11\\ =\left(5x\right)^2-2.5x.1+1^2+10\\ =\left(5x+1\right)^2+10\ge10\forall x\in R\\ Vậy:min_A=10.khi.5x+1=0\Leftrightarrow x=-\dfrac{1}{5}\\ B=\left(x-3\right)^2+\left(11-x\right)^2\\ =\left(x^2-6x+9\right)+\left(121-22x+x^2\right)\\ =x^2+x^2-6x-22x+9+121=2x^2-28x+130\\ =2\left(x^2-14x+49\right)+32\\ =2\left(x-7\right)^2+32\\ Vì:2\left(x-7\right)^2\ge0\forall x\in R\\ Nên:2\left(x-7\right)^2+32\ge32\forall x\in R\\ Vậy:min_B=32.khi.\left(x-7\right)=0\Leftrightarrow x=7\\Tương.tự.cho.biểu.thức.C\)
15 tháng 10 2023
b:
\(D=-25x^2+10x-1-10\)
\(=-\left(25x^2-10x+1\right)-10\)
\(=-\left(5x-1\right)^2-10< =-10\)
Dấu = xảy ra khi x=1/5
\(E=-9x^2-6x-1+20\)
\(=-\left(9x^2+6x+1\right)+20\)
\(=-\left(3x+1\right)^2+20< =20\)
Dấu = xảy ra khi x=-1/3
\(F=-x^2+2x-1+1\)
\(=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1< =1\)
Dấu = xảy ra khi x=1
LN
2 tháng 12 2015
B=\(x^2+3x+7\)
=>B= \(x^2+2\times\frac{3}{2}x+\frac{9}{4}+\frac{19}{4}\)
=>B=\(\left(x+\frac{3}{2}\right)^2+\frac{19}{4}\)
Vì \(\left(x+\frac{3}{2}\right)^2\ge0\) (Với mọi x)
=>\(\left(x+\frac{3}{2}\right)^2+\frac{19}{4}\ge\frac{19}{4}\) (Với mọi x )
Dấu "='' xảy ra <=> \(x+\frac{3}{2}=0=>x=-\frac{3}{2}\)
Vậy min B bằng 19/4 <=>x=-3/2
Phần b thì mk làm đc n phần a hình như sai đề pn ạ !!!
PA
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2023
\(Q=\dfrac{23-10x}{x^2+2}=\dfrac{46-20x}{2\left(x^2+2\right)}=\dfrac{25\left(x^2+2\right)-25x^2-20x-4}{2\left(x^2+2\right)}\)
\(=\dfrac{25}{2}-\dfrac{\left(5x+2\right)^2}{2\left(x^2+2\right)}\le\dfrac{25}{2}\)
\(Q_{max}=\dfrac{25}{2}\) khi \(5x+2=0\Rightarrow x=-\dfrac{2}{5}\)
MH
1
8 tháng 12 2023
a: \(-x^2+10x+3\)
\(=-\left(x^2-10x-3\right)\)
\(=-\left(x^2-10x+25-28\right)\)
\(=-\left(x^2-10x+25\right)+28\)
\(=-\left(x-5\right)^2+28< =28\forall x\)
Dấu '=' xảy ra khi x-5=0
=>x=5
Vậy: GTLN của \(-x^2+10x+3\) là 28 khi x=5
b: \(8x-x^2-16\)
\(=-\left(x^2-8x+16\right)\)
\(=-\left(x-4\right)^2< =0\forall x\)
Dấu '=' xảy ra khi x-4=0
=>x=4
vậy: GTLN của \(8x-x^2-16\) là 0 khi x=4
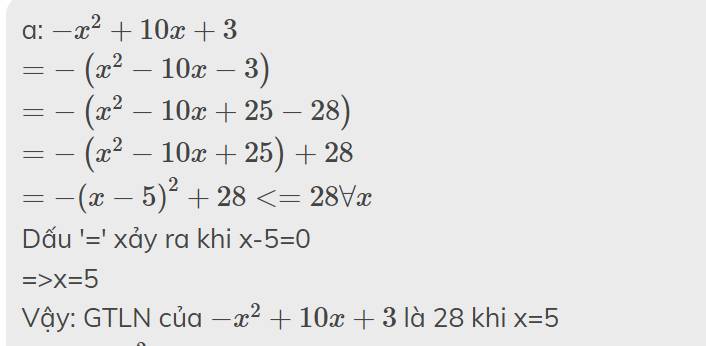
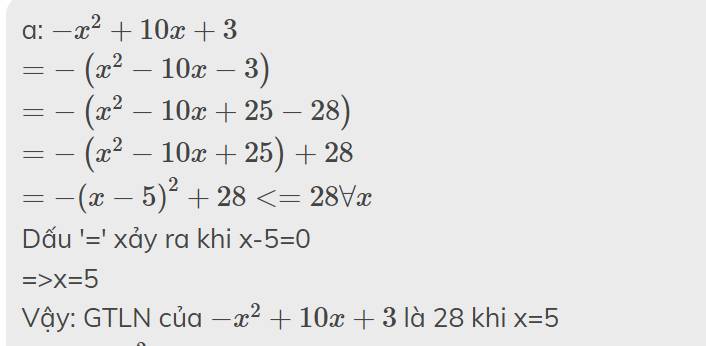
\(3+10x-x^2\\=-(x^2-10x)+3\\=-[x^2-2\cdot x\cdot5+5^2]+25+3\\=-(x-5)^2+28\)
Ta thấy: \(\left(x-5\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-5\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-5\right)^2+28\le28\forall x\)
Dấu \("="\) xảy ra khi: \(x-5=0\Leftrightarrow x=5\)
Vậy GTNN của biểu thức là 28 khi \(x=5\).