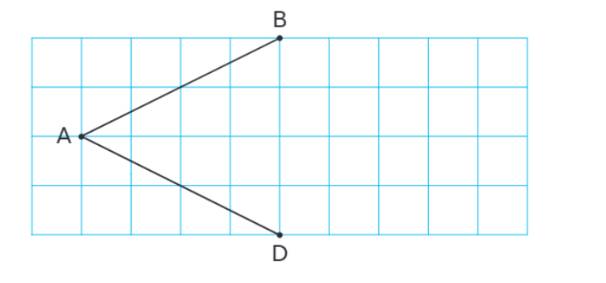
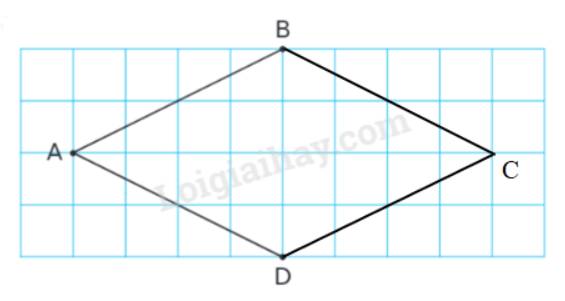
Xác định vị trí điểm C để có hình thoi ABCD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KS
Kiều Sơn Tùng
1 tháng 11 2023
Đúng(0)
Những câu hỏi liên quan
QT
1
13 tháng 6 2023
Diện tích hình thoi ABCD là: 5,4 x 6,8 : 2 = 18,36 (cm2)
Diện tích hình thoi ABCD gấp diện tích hình bình hành AMND số lần là: 18,36 : 6,12 = 3 (lần)
⇒ PN = \(\dfrac{1}{3}\) PC
16 tháng 12 2020
AB=CD,ˆBAM=ˆNCD,AB=CD→ΔAMB=ΔCND(c.g.c)→MB=DNAB=CD,BAM^=NCD^,AB=CD→ΔAMB=ΔCND(c.g.c)→MB=DN
→ˆAMB=ˆDNC→ˆBMN=ˆDNM→BM//DN→◊BNDM→AMB^=DNC^→BMN^=DNM^→BM//DN→◊BNDM là hình bình hành
b.Để ◊BNDM◊BNDM là hình thoi
→MN⊥BD→AC⊥BD→◊ABCD→MN⊥BD→AC⊥BD→◊ABCD là hình thoi
c.Để K là trung điểm AD →AK=KD→AK=KD mà KM//DN→MKM//DN→M là trung điểm AN →AM=MN=NC→AM=MN=NC
T
14 tháng 8 2023
a) Ta có ^A=1/2^ABC nên ^A=60o=>t/gABD đều
=>^D1=^D2=60o
=>^ABD=^HBK=60o=>^B1=^B2
Xét t/gABH và t/gDBK ta có:
AB=BD
^B1=^B2
^A=^D2
=>t/gABD=^DBK(g-c-g)
=>AH=DK mà AD=DC nên
=>HD=KC
=>DH+DK=AD (không đổi)
=>đpcm.
b)Có BH=BK
Lại có: ^HBK=60o=>t/gHBK đều
=>HK nhỏ nhất <=> BH nhỏ nhất
<=>BH_|_AD=>H là trung điểm AD khi đó K cũng là trung điểm của DC
Áp dujnh định lý pi-ta-go ta có:BH2=AB2-AH2=22-12=3=>BH=√33
Vậy H và K để HK ngắn nhất: √3
14 tháng 8 2023
1: ABCD là hình thoi
=>góc A+góc B=180 độ
mà góc B=2*góc A
nên góc A=180/3=60 độ
Xét ΔABD có AB=AD và góc A=60 độ
nên ΔABD đều
2: Xét ΔABH và ΔDBK có
góc BAD=góc BDK
BA=BD
góc ABH=góc DBK
=>ΔABH=ΔDBK
=>AH=DK; BH=BK
Xét ΔBHK có BH=BK và góc HBK=60 độ
nên ΔBHK đều
3: DH+DK=DH+AH=DA ko đổi
PA
17 tháng 11 2016
Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 1800 - AMD = 1800 - CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
=> AMCN là hình bình hành
=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi