giúp mình câu 33 với ạ 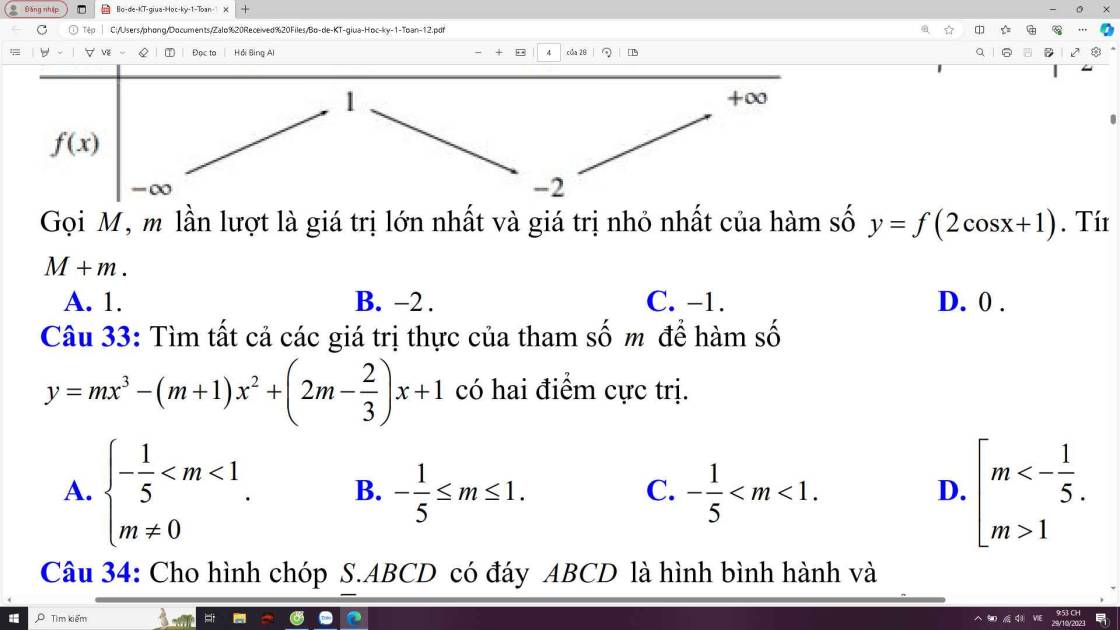
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Ta có \(BD||AC\) (cùng vuông góc AB)
Áp dụng định lý Talet trong tam giác ACE: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b.
Ta có \(IK||BD||AC\) \(\Rightarrow EI||AC\)
Áp dụng Talet: \(\dfrac{DC}{ED}=\dfrac{DA}{ID}\Rightarrow\dfrac{DC}{DC+ED}=\dfrac{DA}{DA+ID}\Rightarrow\dfrac{DC}{CE}=\dfrac{DA}{AI}\) (1)
Do \(BD||EK\), áp dụng Talet trong tam giác CEK: \(\dfrac{BD}{EK}=\dfrac{CD}{CE}\) (2)
Do \(BD||EI\), áp dụng Talet trong tam giác AEI: \(\dfrac{BD}{EI}=\dfrac{AD}{AI}\) (3)
Từ(1);(2);(3) \(\Rightarrow\dfrac{BD}{EK}=\dfrac{BD}{EI}\Rightarrow EK=EI\)

Ta có :
\(\frac{x-3}{97}+\frac{x-27}{73}+\frac{x-67}{33}+\frac{x-73}{27}=4\)
\(\Leftrightarrow\left(\frac{x-3}{97}-1\right)+\left(\frac{x-27}{73}-1\right)+\left(\frac{x-67}{33}-1\right)+\left(\frac{x-73}{27}-1\right)=0\)
\(\Leftrightarrow\frac{x-100}{97}+\frac{x-100}{73}+\frac{x-100}{33}+\frac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\right)=0\)
Vì \(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}>0\) Nên \(x-100=0\)
\(\Leftrightarrow x=100\)
Vậy \(x=100\)
\(\Leftrightarrow\frac{x-3}{87}+\frac{x-27}{79}+\frac{x-67}{33}+\frac{x-73}{27}-4=0\)
\(\Leftrightarrow\left(\frac{x-3}{97}-1\right)+\left(\frac{x-27}{73}-1\right)+\left(\frac{x-67}{33}-1\right)+\left(\frac{x-73}{27}-1\right)=0\)
\(\Leftrightarrow\left(\frac{x-3-97}{97}\right)+\left(\frac{x-27-73}{73}\right)+\left(\frac{x-67-33}{33}\right)+\left(\frac{x-73-27}{27}\right)=0\)
\(\Leftrightarrow\frac{x-100}{97}+\frac{x-100}{73}+\frac{x-100}{33}+\frac{x-100}{27}=0\)
\(\Leftrightarrow\left(x-100\right)\left(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\right)=0\)
Vì \(\frac{1}{97}+\frac{1}{73}+\frac{1}{33}+\frac{1}{27}\ne0\)
\(\Rightarrow x-100=0\Leftrightarrow x=100\)


31.
\(y'=4x^3+1\)
Tiếp tuyến vuông góc với \(d\) nên có hệ số góc \(k=5\)
Gọi hoành độ tiếp điểm là \(x_0\Rightarrow4x_0^3+1=5\Rightarrow x_0^3=1\)
\(\Rightarrow x_0=1\Rightarrow y_0=2\)
Phương trình: \(y=5\left(x-1\right)+2\Leftrightarrow y=5x-3\)
33.
Vận tốc của chất điểm: \(v\left(t\right)=S'\left(t\right)=5-6t\)
\(v\left(t\right)=3\Rightarrow5-6t=3\Rightarrow t=\dfrac{1}{3}\)
\(\Rightarrow S=5.\dfrac{1}{3}-3.\left(\dfrac{1}{3}\right)^2=1,33\left(m\right)\)

Đề trước đó:

(x-7)(x+1)-(x-3)^2=(3x-5)(3x+5)-(3x+1)^2+(x-2)^2-x
<=>x^2+x-7x-7-x^2+6x-9=9x^2-25-9x^2-6x-1+x^2-4x+4-x
<=>x^2-11x-6=0
<=>x^2-2x. 11/2 + 121/4-145/4=0
<=>(x-11/2)^2=145/4
<=>|x-11/2|=căn(145)/2
<=>x=[11+-căn(145)]/2

Bài 4:
a: \(C=\left(\dfrac{1}{3}-\dfrac{1}{2}\right)x^3-2x^2-\left(4+1\right)x+1\)
\(=\dfrac{-1}{6}x^3-2x^2-5x+1\)
b: Thay x=2 vào C, ta được:
\(C=\dfrac{-1}{6}\cdot8-2\cdot4-5\cdot2+1=\dfrac{-4}{3}-8-10+1=\dfrac{-4}{3}-17=\dfrac{-4-51}{3}=-\dfrac{55}{3}\)
Bài 5:
Theo đề, ta có: \(\left(xyz\right)^2=2\cdot6\cdot3=36\)
Trường hợp 1: xyz=6
\(\Leftrightarrow\left\{{}\begin{matrix}z=3\\x=1\\y=2\end{matrix}\right.\)
Trường hợp 2: xyz=-6
\(\Leftrightarrow\left\{{}\begin{matrix}z=-3\\x=-1\\y=-2\end{matrix}\right.\)

a) Xét (O) có
\(\widehat{PFE}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{PFE}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{PFN}=90^0\)
Xét tứ giác PFMN có
\(\widehat{PFN}\) và \(\widehat{PMN}\) là hai góc cùng nhìn cạnh PN
\(\widehat{PFN}=\widehat{PMN}\left(=90^0\right)\)
Do đó: PFMN là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)

a) Xét tam giác ABC và tam giác HBA có:
\(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{ABC}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\)
\(\Rightarrow\dfrac{AB}{BH}=\dfrac{BC}{AB}\Rightarrow AB^2=BC.BH\)
b) Xét tam giác ABC và tam giác HAC có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ACB}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\)
\(\Rightarrow\dfrac{AC}{HC}=\dfrac{BC}{AC}\Rightarrow AC^2=BC.HC\)
c) Ta có: \(\left\{{}\begin{matrix}\Delta ABC\sim\Delta HBA\left(cmt\right)\\\Delta ABC\sim\Delta HAC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta HBA\sim\Delta HAC\)
\(\Rightarrow\dfrac{AH}{CH}=\dfrac{BH}{AH}\Rightarrow AH^2=CH.BH\)
d) Ta có: \(\Delta ABC\sim\Delta HAC\left(cmt\right)\)
\(\Rightarrow\dfrac{AB}{AH}=\dfrac{BC}{AC}\Rightarrow AB.AC=BC.AH\)





 Giúp mình với ạ mình cảm ơn:33
Giúp mình với ạ mình cảm ơn:33



Lời giải:
Để $y$ có 2 điểm cực trị thì:
$y'=3mx^2-2(m+1)x+2m-\frac{2}{3}=0$ có 2 nghiệm phân biệt.
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \Delta'=(m+1)^2-3m(2m-\frac{2}{3})>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ -5m^2+4m+1>0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ (1-m)(5m+1)>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ \frac{-1}{5}< m< 1\end{matrix}\right.\)
Đáp án A.
Dễ vãi cuk