Tìm x, y ϵ \(ℕ\) để 2x-3xy-6x=16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TC
1
AH
Akai Haruma
Giáo viên
24 tháng 9 2023
Lời giải:
a. $2y(3x-1)+9x-3=7$
$2y(3x-1)+3(3x-1)=7$
$(3x-1)(2y+3)=7$
Vì $3x-1, 2y+3$ đều là số nguyên với mọi $x,y\in N$, và $2y+3>0$ nên ta có bảng sau: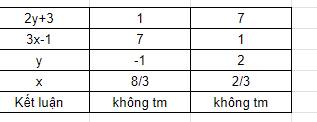
b.
$3xy-2x+3y-9=0$
$x(3y-2)+3y-9=0$
$x(3y-2)+(3y-2)-7=0$
$(3y-2)(x+1)=7$
Đến đây bạn cũng lập bảng tương tự như phần a.
DK
1
DT
29 tháng 12 2021
\(a,=2x^2-\dfrac{3}{2}y+3x\)
\(b,\)bt để chia hết cho x+2 là:\(2x^3+x^2-x+10\)
\(\Rightarrow m=12\)
CL
15 tháng 11 2016
3xy - 5y + 6x = 30
<=> y(3x - 5) + (6x - 10) = 20
<=> y(3x - 5) + 2(3x - 5) = 20
<=> (3x - 5)(y + 2) = 20
Ta có bảng sau:
| 3x - 5 | 1 | -1 | 2 | -2 | 4 | -4 | 5 | -5 | 10 | -10 | 20 | -20 |
| y + 2 | 20 | -20 | 10 | -10 | 5 | -5 | 4 | -4 | 2 | -2 | 1 | -1 |
| x | 2 | 4/3 | 7/3 | 1 | 3 | 1/3 | 10/3 | 0 | 5 | -5/3 | 25/3 | -5 |
| y | 0 | -22 | 8 | -12 | 3 | -7 | 2 | -6 | 0 | -4 | -1 | -3 |
NN
4
17 tháng 7 2021
a) Để y nguyên thì \(6x-4⋮2x+3\)
\(\Leftrightarrow-13⋮2x+3\)
\(\Leftrightarrow2x+3\in\left\{1;-1;13;-13\right\}\)
\(\Leftrightarrow2x\in\left\{-2;-4;10;-16\right\}\)
hay \(x\in\left\{-1;-2;5;-8\right\}\)
29 tháng 8 2023
a: =(a^2-b^2)-(2a-2b)
=(a-b)(a+b)-2(a-b)
=(a-b)(a+b-2)
b: =(3x-3y)+5y(x-y)
=3(x-y)+5y(x-y)
=(x-y)(5y+3)
c: \(=\left(x+y\right)^2\left(x-y\right)+x\left(y-x\right)\)
=(x-y)*(x+y)^2-x(x-y)
=(x-y)[(x+y)^2-x]
d: \(=\left(x-y+4-2x-3y+1\right)\left(x-y+4+2x+3y-1\right)\)
=(-x-4y+5)(3x+2y+3)
e: =16-(x^2-4xy+4y^2)
=16-(x-2y)^2
=(4-x+2y)(4+x-2y)
g: =9x^2-6x+1-(3xy-y)
=(3x-1)^2-y(3x-1)
=(3x-1)(3x-y-1)
h: =(x-y)^3-z^3
=(x-y-z)[(x-y)^2+z(x-y)+z^2]
=(x-y-z)(x^2-2xy+y^2+xz-yz+z^2)
H9
HT.Phong (9A5)
CTVHS
29 tháng 8 2023
a) \(a^2-b^2-2a+2b\)
\(=\left(a^2-b^2\right)-\left(2a-2b\right)\)
\(=\left(a+b\right)\left(a-b\right)-2\left(a-b\right)\)
\(=\left(a-b\right)\left(a+b-2\right)\)
b) \(3x-3y-5x\left(y-x\right)\)
\(=\left(3x-3y\right)+5x\left(x-y\right)\)
\(=3\left(x-y\right)+5x\left(x-y\right)\)
\(=\left(5x+3\right)\left(x-y\right)\)
c) \(x\left(x+y\right)^2-y\left(x+y\right)^2+xy-x^2\)
\(=\left(x+y\right)^2\left(x-y\right)+\left(xy-x^2\right)\)
\(=\left(x+y\right)^2\left(x-y\right)-x\left(x-y\right)\)
\(=\left(x-y\right)\left(x^2+2xy+y^2-x\right)\)
d) \(\left(x-y+4\right)^2-\left(2x+3y-1\right)\)
\(=\left(x-y+4+2x+3y-1\right)\left(x-y+4-2x-3y+1\right)\)
\(=\left(3x+2y+3\right)\left(-x-4y+5\right)\)
Lời giải:
$2x-3xy-6y=16$
$\Rightarrow x(2-3y)-6y=16$
$\Rightarrow x(2-3y)+2(2-3y)=20$
$\Rightarrow (x+2)(2-3y)=20$
Vì $x,y\in\mathbb{N}$ nên $x+2\in N\Rightarrow x+2>0$
Mà $(x+2)(2-3y)=20>0$ nên $2-3y>0$
Mà $2-3y\leq 2-3.0=2$ với mọi $y\in\mathbb{N}, 2-3y$ lẻ nên $2-3y=1$
$\Rightarrow x+2=20; 2-3y=1$
$\Rightarrow x=18; y=\frac{1}{3}$ (loại)
Vậy không tìm được $x,y$ thỏa đề.