bài1 tg ABC vuông tại A ,M là cạnh huyền BC ; D, E là chân đường vuông góc AB, AC a) so sánh AM và DE b) Gọi I là trung điểm DE khi M di chuyển trên BC thì điểm I di chuyển trên đoạn nào vì sao c) tìm vị trí M để BC ngắn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 12 2016
a) Xét t/g AHB và t/g AHC có:
ABH = ACH = 70o (gt)
AB = AC (gt)
Do đó, t/g AHB = t/g AHC ( cạnh huyền góc nhọn) (đpcm)
b) t/g AHB = t/g AHC (câu a) => CAH = BAH (2 góc tương ứng)
=> AH là phân giác BAC (đpcm)
15 tháng 1 2016
Xét tg ABC và tg DEF ta có
góc A=góc D(90 độ)
BC=EF
AB=DE
=>tgDEF=tgABC(c.g.c)
6 tháng 11 2021
a: \(AH=2\sqrt{6}\left(cm\right)\)
\(AB=2\sqrt{10}\left(cm\right)\)
\(AC=2\sqrt{15}\left(cm\right)\)
15 tháng 10 2021
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AH^2=HB\cdot HC\\AC^2=CH\cdot BC\\AB^2=BH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AH=2\sqrt{6}\left(cm\right)\\AC=2\sqrt{15}\left(cm\right)\\AB=2\sqrt{10}\left(cm\right)\end{matrix}\right.\)
17 tháng 9 2023
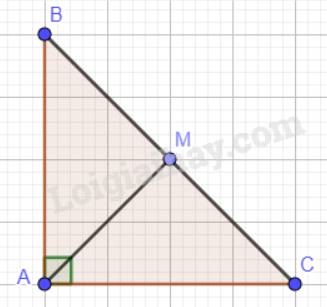
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).
Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).
Xét tam giác ABM và tam giác ACM có:
AB = AC
AM chung
BM = CM
\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)
\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)
Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)
\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).
Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).
Vậy tam giác MAB vuông cân tại M.
a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
=>AM=DE
b: ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
=>I là trung điểm của AM
Gọi H,K lần lượt là trung điểm của AB,AC
Xét ΔABC có
H,K lần lượt là trung điểm của AB,AC
=>HK là đường trung bình
=>HK//BC và HK=BC/2
Xét ΔAMB có
I,H lần lượt là trung điểm của AM,AB
=>IH là đường trung bình
=>IH//MB và IH=MB/2
=>IH//BC
mà KH//BC
nên I,K,H thẳng hàng
=>I di chuyển trên đoạn KH là đường trung bình của ΔABC
bạn ơi thiếu câu c kìa