3x2 -6x+17
x2-2x+5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt và thực hiện phép tính ta có :
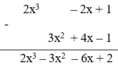
Vậy chọn đa thức thứ hai.

1/ 3-2x+4+6x=x+7+3x
⇔-2x+6x-x-3x=0
⇔0x=0 (Vô số nghiệm)
2/-6(1,5-2x)=3(-15+2x)
⇔-9+12x=-45+6x
⇔6x+36=0
⇔6(x+6)=0
⇔x+6=0
⇔x=-6
Vậy S ϵ {-6}
3/ 3(2x-5)+5(x-1)=4(x+1)
⇔6x-15+5x-5=4x+4
⇔7x=24
⇔x=\(\dfrac{24}{7}\)
Vậy S ϵ {\(\dfrac{24}{7}\)}
1) Ta có: \(3-2x+4+6x=x+7+3x\)
\(\Leftrightarrow4x+7=4x+7\)
\(\Leftrightarrow4x+7-4x-7=0\)
\(\Leftrightarrow0x=0\)(luôn đúng)
Vậy: S={x|\(x\in R\)}
2) Ta có: \(-6\cdot\left(1.5-2x\right)=3\left(-15+2x\right)\)
\(\Leftrightarrow-9+12x=-45+6x\)
\(\Leftrightarrow12x-9+45-6x=0\)
\(\Leftrightarrow6x+36=0\)
\(\Leftrightarrow6x=-36\)
hay x=-6
Vậy: S={-6}
3) Ta có: \(3\left(2x-5\right)+5\left(x-1\right)=4\left(x+1\right)\)
\(\Leftrightarrow6x-15+5x-5=4x+4\)
\(\Leftrightarrow11x-20-4x-4=0\)
\(\Leftrightarrow7x-24=0\)
\(\Leftrightarrow7x=24\)
\(\Leftrightarrow x=\dfrac{24}{7}\)
Vậy: \(S=\left\{\dfrac{24}{7}\right\}\)

a) \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\\6x-5y=27\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}14y=-42\\2x+3y=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x+3.\left(-3\right)=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x-9=-5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\2x=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
Vậy phương trình có nghiệm là: \(\left\{{}\begin{matrix}y=-3\\x=2\end{matrix}\right.\)
b) \(3x^2+4x=0\)
\(\Leftrightarrow x\left(3x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\3x+4=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là: \(S=\left\{0;-\dfrac{4}{3}\right\}\)
c) Đặt: \(x^2=t\left(t\ge0\right)\)
\(\Rightarrow\) Ta có phương trình mới:
\(t^2-3t-4=0\)
Ta có: a - b + c = 1 + 3 - 4 = 0
\(\Rightarrow t_1=-1\left(loại\right);t_2=4\left(TM\right)\)
\(\Rightarrow x=\pm2\)
Vậy tập nghiệm của phương trình là: S = {2; -2}
a, \(\left\{{}\begin{matrix}2x+3y=-5\\6x-5y=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-15\left(1\right)\\6x-5y=27\left(2\right)\end{matrix}\right.\)
Lấy (1) - (2) ta được : \(14y=-15-27=-42\Leftrightarrow y=-3\)
\(\Rightarrow6x-27=-15\Leftrightarrow6x=12\Leftrightarrow x=2\)
Vậy \(\left(x;y\right)=\left(2;-3\right)\)
b, \(3x^2+4x=0\Leftrightarrow x\left(3x+4\right)=0\Leftrightarrow x=0;x=-\dfrac{4}{3}\)
c, \(x^4-3x^2-4=0\Leftrightarrow x^4+x^2-4x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2-4\right)+x^2-4=0\Leftrightarrow\left(x^2+1\right)\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow x=\pm2;x^2+1>0\)
Vậy nghiệm của phương trình là x = -2 ; x = 2

\(1,\\ a,=3x^3-2x^2+5x\\ b,=2x^3y^2+\dfrac{2}{9}x^4y^2-\dfrac{1}{3}x^2y^3\\ c,=x^2-2x+6x-12=x^2+4x-12\\ 2,\\ a,\Rightarrow6x-9+4-2x=-3\\ \Rightarrow4x=2\Rightarrow x=\dfrac{1}{2}\\ b,\Rightarrow5x-2x^2+2x^2-2x=13\\ \Rightarrow3x=13\Rightarrow x=\dfrac{13}{3}\\ c,\Rightarrow5x^2-5x-5x^2+7x-10x+14=6\\ \Rightarrow-8x=-8\Rightarrow x=1\\ d,\Rightarrow6x^2+9x-6x^2+4x-15x+10=8\\ \Rightarrow-2x=-2\Rightarrow x=1\)
\(3,\\ A=2x^2+x-x^3-2x^2+x^3-x+3=3\\ B=6x^2-10x+33x-55-6x^2-14x-9x-21=-76\)

P(x)+Q(x)=3x^2-6x+5
P(x)-Q(x)=x^2+2x-3
=>2P(x)=4x^2-4x+2 và P(x)-Q(x)=x^2+2x-3
=>P(x)=2x^2-2x+1 và Q(x)=2x^2-2x+1-x^2-2x+3=x^2-4x+4

a) 6x³ : (-3x²) = [6 : (-3)] . (x³ : x²)
= -2x
b) (-9x²) : 6x
= (-9 : 6) . (x² : x)
= -3/2 x
c) (-16x⁴) : (-12x³)
= [-16 : (-12)] . (x⁴ : x³)
= 4/3 x
d) (8x³ + 4x² - 6x) : 2x
= 8x³ : 2x + 4x² : 2x - 6x : 2x
= 4x² + 2x - 3

Lời giải:
$A(x)+B(x)=5-3x^2+2x-5x^3+6x+7x^3-7x^2-9$
$=2x^3-10x^2+8x-4$
$A(x)-B(x)=(5-3x^2+2x-5x^3)-(6x+7x^3-7x^2-9)$
$=-12x^3+4x^2-4x+14$
đề bài là phân tích đa thức thành nhân tử đúng ko??