Giúp mình giải nhanh với được không ạ...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
T
.thuyanh
5 tháng 10 2023
Đúng(0)
Những câu hỏi liên quan
24 tháng 6 2024
Câu 6: Để hàm số y=(1-m)x+3 nghịch biến trên R thì 1-m<0
=>m>1
=>Chọn B
Câu 7: D
Câu 10: (D)//(D')
=>\(\left\{{}\begin{matrix}3m+1=2\left(m+1\right)\\-2\ne-2\left(loại\right)\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
=>Chọn D
Câu 11: \(x^2+2x+2=\left(x+1\right)^2+1>=1>0\forall x\)
=>\(\sqrt{x^2+2x+2}\) luôn xác định với mọi số thực x
=>Chọn A
Câu 12: Để hai đường thẳng y=x+3m+2 và y=3x+2m+3 cắt nhau tại một điểm trên trục tung thì \(\left\{{}\begin{matrix}1\ne3\left(đúng\right)\\3m+2=2m+3\end{matrix}\right.\)
=>3m+2=2m+3
=>m=1
=>Chọn C
NA
1
4 tháng 9
Bài 3:
a: \(7x\left(\frac17x-5\right)+2\cdot\left(8-\frac12x^2\right)=21\)
=>\(x^2-35x+16-x^2=21\)
=>-35x=21-16=5
=>\(x=-\frac{5}{35}=-\frac17\)
b: \(5x\left(\frac45x+3\right)-2x\left(2x-1\right)=17\)
=>\(4x^2+15x-4x^2+2x=17\)
=>17x=17
=>x=1
c: \(12\left(x^2-3x+1\right)+2x\left(1-6x\right)=x-2\)
=>\(12x^2-36x+12+2x-12x^2=x-2\)
=>-34x+12=x-2
=>-35x=-14
=>\(x=\frac{14}{35}=\frac25\)
d: ,\(12x^2-2x\left(6x-5\right)=11x-31\)
=>\(12x^2-12x^2+10x=11x-31\)
=>11x-31=10x
=>x=31
Bài 2:
a: \(A=x\left(6x^2+2x\right)-6x^3-2x^2-11\)
\(=6x^3+2x^2-6x^3-2x^2-11\)
=-11
b: \(B=12x\left(x-5\right)-12\left(x^2-4x\right)+12x+17\)
\(=12x^2-60x-12x^2+48x+12x+17\)
=17
c: \(C=8x\left(x^2-x\right)-x^2\left(8x-8\right)+31\)
\(=8x^3-8x^2-8x^3+8x^2+31\)
=31
d: \(D=6x\left(x^2-7x+2\right)-6\left(x^3-7x^2+2x-35\right)\)
\(=6x^3-42x^2+12x-6x^3+42x^2-12x+210\)
=210
e: \(E=11\left(x^2-5x+3\right)-x\left(11x-55\right)+19\)
\(=11x^2-55x+33-11x^2+55x+19\)
=33+19
=52
f: \(F=4x^2-4x-4x\left(x-1\right)-15\)
=4x(x-1)-4x(x-1)-15
=-15
Bài 1:
a: \(2x\left(x-3\right)-2x^2\)
\(=2x^2-6x-2x^2\)
=-6x
b: -x(2x+5)+10x
\(=-2x^2-5x+10x\)
\(=-2x^2+5x\)
c: \(2x^2\left(x^3-5x+1\right)-2x^3\left(x^2-5\right)\)
\(=2x^5-10x^3+2x^2-2x^5+10x^3=2x^2\)
d: \(2x^2-2x^2\left(x^2+x-5\right)\)
\(=2x^2\left(1-x^2-x+5\right)=2x^2\left(-x^2-x+6\right)=-2x^4-2x^3+12x^2\)
e: \(5xy-xy\left(x^2-2xy-1\right)=xy\left(5-x^2+2xy+1\right)=xy\left(-x^2+2xy+6\right)\)
\(=-x^3y+2x^2y^2+6xy\)
f: \(5x^3y-x^2y\left(xy+5x+1\right)\)
\(=5x^3y-x^3y^2-5x^3y-x^2y=-x^3y^2-x^2y\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 7 2021
1.
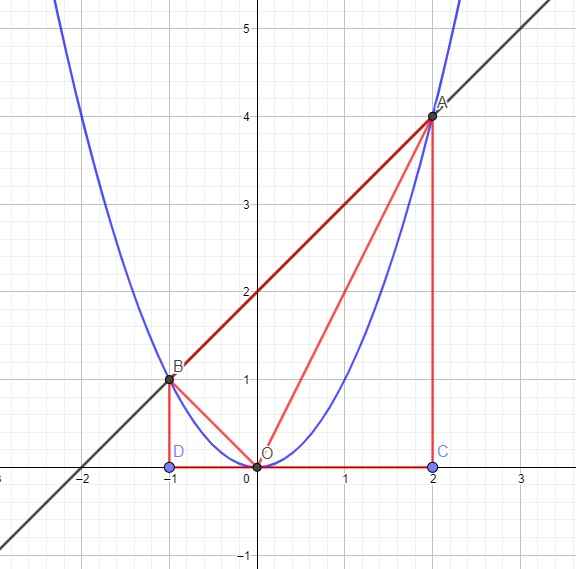
Dễ dàng tìm được tọa độ 2 giao điểm, do vai trò của A, B như nhau, giả sử \(A\left(2;4\right)\) và \(B\left(-1;1\right)\)
Gọi C và D lần lượt là 2 điểm trên trục Ox có cùng hoành độ với A và B, hay \(C\left(2;0\right)\) và \(D\left(-1;0\right)\)
Khi đó ta có ABDC là hình thang vuông tại D và C, các tam giác OBD vuông tại D và tam giác OAC vuông tại C
Độ dài các cạnh: \(BD=\left|y_B\right|=1\) ; \(AC=\left|y_A\right|=4\)
\(OD=\left|x_D\right|=1\) ; \(OC=\left|x_C\right|=2\) ; \(CD=\left|x_C-x_D\right|=3\)
Ta có:
\(S_{OAB}=S_{ABDC}-\left(S_{OBD}+S_{OAC}\right)\)
\(=\dfrac{1}{2}CD.\left(AC+BD\right)-\left(\dfrac{1}{2}BD.OD+\dfrac{1}{2}AC.OC\right)\)
\(=\dfrac{1}{2}.3.\left(4+1\right)-\left(\dfrac{1}{2}.1.1+\dfrac{1}{2}.4.2\right)=3\)
DQ
1
8 tháng 4 2022
Câu 4:
Thay x=2 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)
Các bạn giải giúp mình với ạ, phần a ghi chi tiết bước giải hộ mình nhé. Mình cám ơn ạ! (Mai mình nộp rồi nên nhanh giúp mình ạ T.T)
13 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{10;-10;\sqrt{10};-\sqrt{10}\right\}\)
b: \(A=\dfrac{5x^3+50x+2x^2+20+5x^3-50x-2x^2+20}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
\(=\dfrac{10x^3+40}{\left(x^2-10\right)\left(x^2+10\right)}\cdot\dfrac{x^2-100}{x^2+4}\)
