chung minh : a2b2(a2+b2) < 128 với a,b>0 và a+b=4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 7 2017
a) ab a 2 − b 2 − a 2 b 2 − a 2 = a a − b
b) 1 u − 6 u 2 − 36 u − 18 36 u 2 − 1 = 1 − 6 u u ( 1 + 6 u )
C
1
TC
1
27 tháng 10 2023
b: \(xy\left(x+y\right)-yz\left(y+z\right)+xz\left(x-z\right)\)
\(=x^2y+xy^2-y^2z-yz^2+x^2z-xz^2\)
\(=x^2y-yz^2+xy^2-y^2z+x^2z-xz^2\)
\(=y\left(x-z\right)\left(x+z\right)+y^2\left(x-z\right)+xz\left(x-z\right)\)
\(=\left(x-z\right)\left(xy+yz+y^2+xz\right)\)
\(=\left(x-z\right)\left(x+y\right)\left(x+z\right)\)
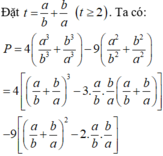
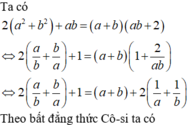
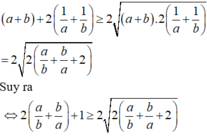
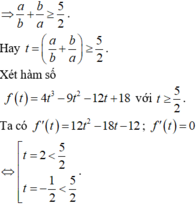
Lời giải:
Áp dụng BĐT AM-GM:
$A=a^2b^2(a^2+b^2)$
$4A=2ab.2ab(a^2+b^2)\leq \left(\frac{2ab+2ab+a^2+b^2}{3}\right)^3$
$=[\frac{(a+b)^2+2ab}{3}]^3=(\frac{16+2ab}{3})^3$
Mà:
$2ab\leq 2(\frac{a+b}{2})^2=2(\frac{4}{2})^2=8$
$\Rightarrow 4A\leq (\frac{16+8}{3})^3=512$
$\Rightarrow A\leq 128$
Dấu "=" xảy ra khi $a=b=2$