Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
a)
b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị
c) Khoảng cách từ điểm - 5 đến điểm 0 là: 5 đơn vị
TL
4
25 tháng 12 2016
Khoảng cách từ điểm 6 đến điểm -2 trên trục số là :
+( 6 + 2 ) = 8
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
Hai điểm biểu diễn các số hữu tỉ \(\frac{5}{4}\) và \(\frac{{ - 5}}{4}\) cách gốc 0 một khoảng bằng nhau.
VT
5 tháng 1 2018
Đáp án B
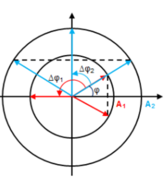
Biểu diễn hai dao động như hình vẽ.
- Tại t = 0 khoảng cách hai điểm sáng là
- Sau khoảng thời gian ∆t điểm sáng 1 quay được góc 
và điểm sáng 2 quay được góc 
Do sau khoảng thời gian 2∆t điểm sáng 1 lại trở về vị trí ban đầu nên sau khoảng thời gian ∆t thì dao động 1 có pha là π rad.
Hai dao động khi đó vuông góc và điểm sáng 2 châm hơn nên vị trí được biểu diễn như hình.
Lúc này ta có khoảng cách giữa hai điểm sáng là A1 = 2a
- Sau khoảng thời gian 2∆t điểm sáng 1 quay được thêm một góc 
nữa và điểm sáng 2 quay được thêm một góc 
nữa. Vị trí của chúng được biểu diễn như hình.
Khoảng cách giữa chúng là
bằng
VT
22 tháng 12 2017
Đáp án B
Biểu diễn hai dao động như hình vẽ.
- Tại 
khoảng cách hai điểm sáng là 
- Sau khoảng thời gian ∆t điểm sáng 1 quay được góc 
và điểm sáng 2 quay được góc 
Do sau khoảng thời gian 2∆t điểm sáng 1 lại trở về vị trí ban đầu nên sau khoảng thời gian ∆t thì dao động 1 có pha là π rad.
Hai dao động khi đó vuông góc và điểm sáng 2 châm hơn nên vị trí được biểu diễn như hình.
Lúc này ta có khoảng cách giữa hai điểm sáng là 
- Sau khoảng thời gian 2∆t điểm sáng 1 quay được thêm một góc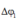 
nữa và điểm sáng 2 quay được thêm một góc 
nữa. Vị trí của chúng được biểu diễn như hình.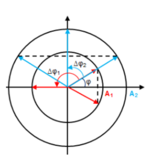 
Khoảng cách giữa chúng là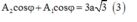 
Từ 
VT
6 tháng 2 2019
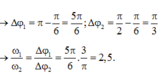
Đáp án D
Khi dịch chuyển nguồn theo phương song song với hai khe thì hệ vân (vân trung tâm ) dịch chuyển theo chiều ngược lại một đoạn :
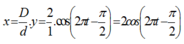
Chu kì dao động là : T = 1s.
Khoảng vân :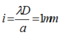 
Điểm M cách vị trí trung tâm 1mm, vậy ban đầu khi t = 0 thì M là vân sáng.
Điểm M là vân sáng thì thỏa mãn : xM = ki
Ta thấy vân trung tâm sẽ dao động với biên độ 2 cm (từ phương trình), vậy điểm M sẽ là vân sáng khi vân trung tâm ở các vị trí có tọa độ x = 0, 1, 2, – 1, –2 cm
Vẽ đường tròn ta được:
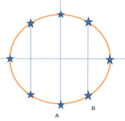
Các vị trí đánh dấu sao là các vị trí trong một chu kì chuyển động M là vân sáng. Ban đầu M nằm ở vị trí A. mỗi chu kì có 8 lần M là vân sáng
Vậy khi M à vân sáng lần thứ 2018 = 8.252 + 2 lần thì nó đã đi trong thời gian là : t = 252T + ∆t
Dễ thấy khi đi được 252 chu kì thì M đã quay lại A, vậy chỉ cần đi đến B là đã được thêm 2 lần nữa ( vì ban đầu khi t = 0 thì M ở A, nên nó là 1 vân sáng, đến lúc nó đến B được tính là lần nữa).
Thời gian đi hết cung AB là :
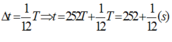
Ta thấy khoảng cách từ 0 đến điểm \(\sqrt 2 \) bằng \(\sqrt 2 \).
Khoảng cách từ 0 đến điểm -\(\sqrt 2 \) bằng \(\sqrt 2 \)
Vậy khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \) bằng nhau.
Khoảng cách từ điểm 0 đến điểm √22 là √22.
Khoảng cách từ điểm 0 đến điểm -√22 là √22.
Do đó khoảng cách từ điểm 0 đến điểm √22 và khoảng cách từ điểm 0 đến điểm −√2-2 là bằng nhau vì đều bằng √22.