Tìm số đo:
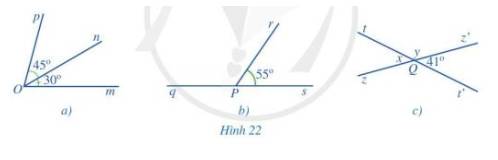
a) Góc mOp trong Hình 22a;
b) Góc qPr trong Hình 22b;
c) x,y trong Hình 22c.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

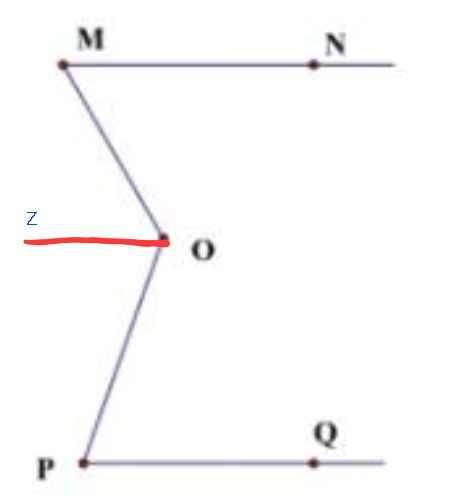 Vẽ tia Oz //MN
Vẽ tia Oz //MN
⇒ ∠MOz = ∠OMN = 60⁰
⇒ ∠zOP = ∠MOP - ∠MOz
= 130⁰ - 60⁰
= 70⁰
Để MN // PQ thì MN // Oz
⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)

Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)

vi moq=90
mop=90
nen moq=mop
to ko chac chan voi phan nay dau do con phan b to chua nhgi ra


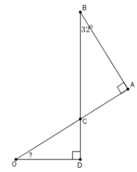
Ta có tam giác ABC vuông ở A nên

Tam giác OCD vuông ở D nên
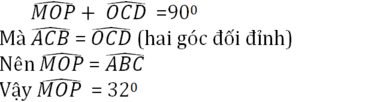
a) Vì tia On nằm trong góc mOp nên \(\widehat {mOn} + \widehat {nOp} = \widehat {mOp}\)
\(\begin{array}{l} \Rightarrow 30^\circ + 45^\circ = \widehat {mOp}\\ \Rightarrow 75^\circ = \widehat {mOp}\end{array}\)
Vậy số đo góc mOp là 75 độ
b) Ta có: \(\widehat {q\Pr } + \widehat {rPs} = 180^\circ \) (2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {q\Pr } + 55^\circ = 180^\circ \\ \Rightarrow \widehat {q\Pr } = 180^\circ - 55^\circ = 125^\circ \end{array}\)
Vậy số đo góc qPr là 125 độ
c) Ta có: \(\widehat {tQz} = \widehat {t'Qz'}\) ( 2 góc đối đỉnh), mà \(\widehat {t'Qz'} = 41^\circ \Rightarrow \widehat {tQz} = 41^\circ \)
\(\widehat {tQz'} + \widehat {z'Qt'} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tQz'} + 41^\circ = 180^\circ \Rightarrow \widehat {tQz'} = 180^\circ - 41^\circ = 139^\circ \)
Vậy x = 41 \(^\circ \) ; y = 139 \(^\circ \)