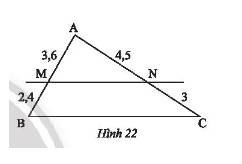
Quan sát Hình 22, chứng minh rằng \(MN//BC\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) BA là đường vuông góc;
BM và BC là các đường xiên kẻ từ B đến đường thẳng AC
Ta được đường ngắn nhất là đường thẳng vuông góc nên BA là đoạn ngắn nhất.
b) Tương tự câu a
MA là đường vuông góc;
MN và MB là các đường xiên kẻ từ M đến đường thẳng AB
Ta được đường ngắn nhất là đường thẳng vuông góc nên MA là đoạn ngắn nhất.
c) Xét tam giác ABC vuông tại A
\( \Rightarrow \widehat A = {90^o}\)\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \) BC > AC ( định lí về góc đối diện và cạnh )
Vì M nằm giữa AC nên AM < AC
\( \Rightarrow \) AM < AC < BC
Vậy AM < BC
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Xét tam giác ABD và tam giác ACD có :
AB = AC ( giả thiết )
BD = CD ( giả thiết )
AD cạnh chung
\( \Rightarrow \Delta ABD =\Delta ACD (c-c-c)\)
\( \Rightarrow \)\(\widehat {BAD} = \widehat {CAD}\)( 2 góc tương ứng )
Xét tam giác ABM và ta giác ACM có :
AB = AC ( giả thiết )
AM cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)( chứng minh trên )
\(\Delta ABM=\Delta ACM (c-g-c)\)
\(\Rightarrow MC = MB\) ( 2 cạnh tương ứng )
\( \Rightarrow \) M là trung điểm BC
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
Xét tam giác BCD có BD = CD ( giả thiết )
\( \Rightarrow \) D thuộc trung trực BC do cách đều 2 đầu mút đoạn BC
Mà AM là trung trực của BC
\( \Rightarrow \) D thuộc đường thẳng AM
\( \Rightarrow \) A, M, D thẳng hàng
B
1
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
Xét \(\Delta HAE\) và \(\Delta FBE\) ta có:
\(AH = BF\) (gt)
\(\widehat {{\rm{HAE}}} = \widehat {{\rm{FBE}}} = 90^\circ \) (gt)
\(AE = BE\) (gt)
Suy ra \(\Delta HAE = \Delta FBE\) (c-g-c)
Suy ra \(HE = EF\)
Chứng minh tương tự ta có: \(EF = GF\); \(GF = GH\); \(GH = HE\)
Suy ra \(HE = EF = FG = GH\)
Suy ra \(EFGH\) là hình thoi
CM
27 tháng 1 2019
a) Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
b) Hình 86a) Hai đường tròn tiếp xúc ngoài thì A nằm giữa O và O’
Hình 86b) Hai đường tròn tiếp xúc trong thì A nằm ngoài đoạn OO’
CM
5 tháng 1 2018
Ta có: OA = OB (= bán kính đường tròn (O))
O’A = O’B (= bán kính đường tròn (O’))
⇒ OO’ là đường trung trực của AB
PT
1
CM
11 tháng 10 2018
*Ta có B O N ^ = P O x ^ = 45 ° (đối đỉnh) suy ra B O N ^ + O N M ^ = 135 ° + 45 ° = 180 ° mà 2 góc này ở vị trí trong cùng phía nên MN // BO.
* B C ⊥ B O B C ⊥ C P ⇒ B O / / C P ( từ vuông góc đến song song) mà B O / / M N = > ⇒ B O / / M N / / C P (ba đường thẳng song song)
* B C ⊥ C P C P / / M N ⇒ M N ⊥ B C ( từ song song đến vuông góc)
PT
1
CM
2 tháng 8 2018
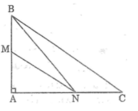
Nối BN.
+ Ta có: AM < AB
Mà NM, NB là các đường xiên ứng với hình chiếu AM, AB
⇒ NM < NB (1)
+ Lại có AN < AC.
Mà BN, BC là các đường xiên ứng với hình chiếu AN, AC
⇒ BN < BC (2)
Từ (1) và (2) suy ra: MN < BC
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
a) Vì Cx // AB nên \(\widehat {ABC} = \widehat {BCx}\) ( 2 góc so le trong), mà \(\widehat {ABC} = 45^\circ \Rightarrow \widehat {BCx} = 45^\circ \)
b) Vì AE \( \bot \) AB; AE \( \bot \) ED nên AB // ED (2 đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song với nhau)
Mà Cx // AB (gt)
\( \Rightarrow \) Cx // ED (2 đường thẳng cùng song song với đường thẳng thứ ba thì thì song song với nhau)
c) Vì Cx // ED nên \(\widehat {EDC} = \widehat {DCx}\) ( 2 góc so le trong), mà \(\widehat {EDC} = 60^\circ \Rightarrow \widehat {DCx} = 60^\circ \)
Vì tia Cx nằm trong góc BCD nên \(\widehat {BCD} = \widehat {BCx} + \widehat {DCx} = 45^\circ + 60^\circ = 105^\circ \)
Ta có:
\(\frac{{AM}}{{MB}} = \frac{{3,6}}{{2,4}} = \frac{3}{2}\);\(\frac{{AN}}{{NC}} = \frac{{4,5}}{3} = \frac{3}{2}\).
Vì \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} = \frac{3}{2}\)
Theo định lí Thales đảo trong \(\Delta ABC\), ta có \(MN//BC\) (điều phải chứng minh).