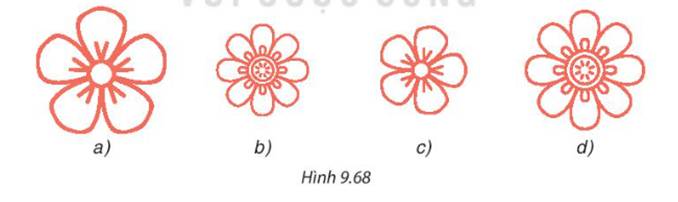
Biết rằng mỗi hình dưới đây đồng dạng với một hình khác, hãy tìm các cặp hình đồng dạng đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(chú ý: bài toán này là tìm 1 đồng nhẹ hơn, nếu nặng hơn cứ thay vô mà tính,
TH: trường hợp.)
Giải
Ta lấy 12 đồng đem lên cân, sẽ có 2 TH:
TH1: Nếu hai cân bằng nhau tức là đồng còn lại có khối lượng khác vs các đồng còn lại => Tìm đc đồng "lạc loài" vs 1 lần cân
TH2: Nếu 2 cân k bằng nhau thì ta lấy bên nhẹ hơn, cân 6 đồng (mỗi bên 3 đồng) , sẽ có 1 bên nhẹ hơn, ta lấy bên nhẹ hơn ấy rồi đặt 2 đồng bất kì lên cân, ta lại có 2 TH:
TH1: Nếu cân thăg bằng thì đồng còn lại là đồng "giả" => Tìm đc vs 3 lần cân
TH2: Nếu cân k thăg bằng thì đồng nhẹ hơn là đông "giả" => Tìm đc vs 3 lần cân

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB 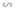 ΔFDC (1)
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB 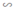 ΔDEA (2)
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA 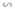 ΔFDC (tính chất)
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB 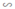 ΔDEA
ΔDEA
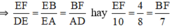
⇒ EF = 5cm, BF = 3,5cm.

a) Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác mới đồng dạng với tam giác đã cho.
ΔFCD có EB // CD (E ∈ FD, B ∈ FC)
⇒ ΔFEB 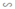 ΔFDC (1)
ΔFDC (1)
ΔAED có FB // AD (F ∈ DE, B ∈ AE)
⇒ ΔFEB 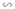 ΔDEA (2)
ΔDEA (2)
Từ (1) và (2) suy ra: ΔDEA 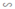 ΔFDC (tính chất)
ΔFDC (tính chất)
b) AB = 12cm, AE = 8cm
⇒ EB = AB – AE = 12 - 8 = 4cm.
Vì ABCD là hình bình hành nên AD = BC = 7cm
Do ΔFEB 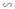 ΔDEA
ΔDEA
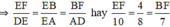
⇒ EF = 5cm, BF = 3,5cm.

Sơ đồ hóa phép lai:
P: cây hạt vàng, vỏ trơn, hình dạng hạt tròn (A-B-D-) x cây hạt xanh, vỏ trơn, hình dạng hạt tròn (aaB-D-)
F1: 8 loại kiểu hình, hạt vàng, vỏ trơn, hình dạng hạt tròn (A-B-D-) chiếm 27 80
Do F1 thu đuợc 8 loại kiểu hình, do đó kiểu gen dự tính của (P) phải là
(AaBb)Dd x(aaBb)Dd
→ Tỉ lệ kiểu hình hạt vàng, vỏ trơn
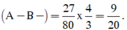
Xét phép lai A a B b × a B a b
(Đối với kiểu gen di truyền liên kết, khi chưa rõ là dị hợp đều hay dị hợp chéo thì ta kí hiệu vào ngoặc đơn)

Thật ra vẫn có tỉ lệ tương quan kiểu hình cho phép lai giữa 1 cơ thể dị hợp 2 cặp gen với 1 cơ thể dị hợp 1 cặp gen dạng A a B b × a B a b nhưng bản thân tôi thấy rằng nó là 1 phần rất nhỏ nên không cần phải máy móc công thức.
(1) Đúng. Xét phép lai
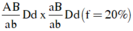
đời con thu được số kiểu gen tối đa là: 7.3 = 21
(2) Đúng. Tỉ lệ cây hạt vàng, vỏ nhăn, hình dạng hạt tròn có kiểu gen đồng hợp
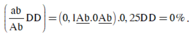
(3) Sai. Tỉ lệ kiểu gen mang 3 cặp dị hợp thu được ở đời con F1 là 12,5%, trong đó:

(4) Sai. Tỉ lệ kiểu hình hạt xanh, vỏ trơn, hình dạng hạt tròn chiếm tỉ lệ 22,5%
Đáp án B

Đáp án B
Sơ đồ hóa phép lai:
P: cây hạt vàng, vỏ trơn, hình dạng hạt tròn (A-B-D-) x cây hạt xanh, vỏ trơn, hình dạng hạt tròn (aaB-D-)
F1: 8 loại kiểu hình, hạt vàng, vỏ trơn, hình dạng hạt tròn (A-B-D-) chiếm 27 80
Do F1 thu đuợc 8 loại kiểu hình, do đó kiểu gen dự tính của (P) phải là
(AaBb)Dd x(aaBb)Dd
→ Tỉ lệ kiểu hình hạt vàng, vỏ trơn ![]()
Xét phép lai ![]() (Đối với kiểu gen di truyền liên kết, khi chưa rõ là dị hợp đều hay dị hợp chéo thì ta kí hiệu vào ngoặc đơn)
(Đối với kiểu gen di truyền liên kết, khi chưa rõ là dị hợp đều hay dị hợp chéo thì ta kí hiệu vào ngoặc đơn)

→ Tỉ lệ kiểu hình hạt vàng, vỏ trơn ![]()
![]()
Thật ra vẫn có tỉ lệ tương quan kiểu hình cho phép lai giữa 1 cơ thể dị hợp 2 cặp gen với 1 cơ thể dị hợp 1 cặp gen dạng ![]() nhưng bản thân tôi thấy rằng nó là 1 phần rất nhỏ nên không cần phải máy móc công thức.
nhưng bản thân tôi thấy rằng nó là 1 phần rất nhỏ nên không cần phải máy móc công thức.
(1)Đúng. Xét phép lai ![]() đời con thu được số kiểu gen tối đa là: 7.3 = 21
đời con thu được số kiểu gen tối đa là: 7.3 = 21
(2) Đúng. Tỉ lệ cây hạt vàng, vỏ nhăn, hình dạng hạt tròn có kiểu gen đồng hợp ![]()
(3) Sai. Tỉ lệ kiểu gen mang 3 cặp dị hợp thu được ở đời con F1 là 12,5%, trong đó: 
(4) Sai. Tỉ lệ kiểu hình hạt xanh, vỏ trơn, hình dạng hạt tròn chiếm tỉ lệ:
a
B
a
-
D
-
=
0
,
1
a
B
.
(
0
,
5
a
b
+
0
,
5
a
B
)
+
0
,
4
a
b
.
0
,
5
a
B
.
0
,
75
D
-
=
22
.
5
%

Ta có:
AC/BC = 3/4,5 = 2/3
DE/EF = 2/3
⇒ AC/BC = DE/EF
∆ABC và ∆DFE có:
AC/BC = DE/EF = 2/3
∠BAC = ∠EDF = 90⁰
⇒ ∆ABC ∽ ∆DFE (cạnh huyền - cạnh góc vuông)
Tam giác ABC và tam giác DEF có:
\( \widehat A = \widehat D = 90^0 \)
\( \frac {AC}{DE} = \frac {BC}{EF} = \frac {3}{2} \)
\( \Rightarrow \Delta ABC \backsim \Delta DFE (ch - cgv) \)

Trong hình bên có 3 cặp tam giác đồng dạng là BHA và BAC; CHA và CAB; HAB và HCA.

a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB - AE = 12 - 8 = 4cm
∆ADE ∽ ∆BFE => =
=
=> =
=
=> BF = 3,5 cm.
EF = 5 cm.
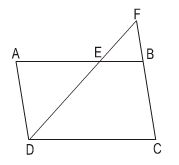
a) BE // DC => ∆BEF ∽ ∆CDF
AD // BF => ∆ADE ∽ ∆BFE.
Do đó: ∆ADE ∽ ∆CFD
b) BE = AB – AE = 12 – 8 = 4cm
∆ADE ∽ ∆BFE =>\(\frac{AE}{BE}=\frac{AD}{BF}=\frac{DE}{EF}\)
\(\Rightarrow\frac{8}{4}=\frac{7}{BF}=\frac{10}{EF}\)
\(\Rightarrow BF=3,5cm\)
\(\Rightarrow EF=5cm\)

a) ΔABC  ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔHBA vì Â = Ĥ = 90º, B̂ chung
ΔABC 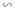 ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHAC vì Â = Ĥ = 90º, Ĉ chung
ΔHBA 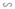 ΔHAC vì cùng đồng dạng với ΔABC.
ΔHAC vì cùng đồng dạng với ΔABC.
b) + ΔABC vuông tại A
⇒ BC2 = AB2 + AC2
(Theo định lý Pytago)


- △ ABC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ở đỉnh B chung
- △ ABC đồng dạng △ HAC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ ABC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ NMC
Hai tam giác vuông có góc nhọn ở đỉnh C chung
- △ HAC đồng dạng △ HBA
Hai tam giác vuông có góc nhọn ∠ (HBA) = ∠ (HAC)
- △ HAB đồng dạng △ NCM
Hai tam giác vuông có góc nhọn ∠ (HAB) = ∠ (NCM)
Cặp hình đồng dạng: a và c, b và d