Tìm a thuộc N để (2a-1)(a^2+2a+15) là số nguyên tố
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài giải:
2a+5 <20 => a < 15/2
=> 0< a <8 ; Lưu ý rằng 0 không phải là số nguyên tố.
Các số nguyên tố có trong khoảng (0;8) là 1, 2, 3, 5, 7
thì lúc đó (2a+5) lần lượt là 7, 9, 11, 15, 19. Trong đó có 7,11,19 là số nguyên tố.
Vậy a = 1, 3, 7
3;4;7;9;12;13;14;16;17;18;19
Ta thu lai :
2a+5=>2.3+5=11
2a+5=>2.4+5=13
2a+5=>2.7+5=19
2a+5=>2.9+5=23
2a+5=>2.12+5=29
2a+5=>2.13+5=31
2a+5=>2.14+5=33
2a+5=>2.16+5=37
2a+5=>2.17+5=39
2a+5=>2.18+5=41
2a+5=>2.19+5=43
mìh ko chắc lắm

1.Với a = 2 ta có 2a + 1 = 5 không thích hợp
Với a ≠ 2 do a là số nguyên tố nên a lẽ
Vậy 2a + 1 là lập phương của một số lẽ nghĩa là
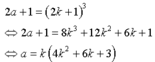
Từ đó k là ước của a. Do k là số nguyên tố nên k = 1 hoặc k = a
-Nếu k = 1 thì 2a + 1 = (2.1 + 1)3 suy ra a = 13 thớch hợp
- Nếu a = k từ a = a(4a2 + 6a + 3) do a là nguyên tố nên suy ra
1 = 4a2 + 6a + 3 không có số nguyên tố a nào thoả món phương trỡnh này Vì vế phải luụn lớn hơn 1
Vậy a = 13
2.Giả sử

13 và p là các số nguyên tố , mà n – 1 > 1 và n2 + n + 1 > 1
Nên n – 1 = 13 hoặc n – 1 = p
- Với n – 1 =13 thì n = 14 khi đó 13p = n3 – 1 = 2743 suy ta p = 211 là số nguyên tố
- Với n – 1 = p thi n2 + n + 1 = 13 suy ra n = 3 . Khi đó p = 2 là số nguyên tố
Vậy p = 2, p = 211 thì 13p + 1 là lập phương của một số tự nhiên

Bài 1
Bốn số nguyên tố có 2 chữ số lần lượt là:
11; 13; 17; 19
Câu 2:
Tìm a để 2a là số nguyên tố
Vì 2a là số chẵn với mọi a. Mà số chẵn duy nhất là nguyên tố là số 2
Vậy 2a = 2
a = 2: 1
a = 1
Vậy a = 1
Lời giải:
Để $(2a-2)(a^2+2a+15)$ là snt thì buộc 1 trong 2 thừa số đã cho phải là 1 còn thừa số còn lại là snt.
Hiển nhiên $a^2+2a+15>1$ với mọi $a\in\mathbb{N}$ nên $2a-1=1$
$\Rightarrow a=1$.
Thay $a=1$ vào thì $(2a-1)(a^2+2a+15)=18$ không phải snt.
Vậy không tồn tại $a$ thỏa mãn đề.
\(\left(2a-1\right)\left(a^2+2a+15\right)\left(a\inℕ\right)\)
Đẻ \(\left(2a-1\right)\left(a^2+2a+15\right)\) là số nguyên tố khi và chỉ khi
\(\left\{{}\begin{matrix}2a-1⋮1\\a^2+2a+15⋮1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2a-1=1\\a^2+2a+15=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2a=2\\a^2+2a+15=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=1\\1^2+2.1+15=1\left(vô.lý\right)\end{matrix}\right.\)
\(\Rightarrow a\in\varnothing\)