cho tanα = \(\dfrac{3}{4}\)
tính sinα, cosα, cotα
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3

ta có :\(\sin2=\dfrac{\sqrt{3}}{2}\Rightarrow2=60^0\)
\(\cos60^o=\dfrac{1}{2};\tan60^o=\sqrt{3};\cot60^o=\dfrac{1}{\sqrt{3}}\)

$\sin \alpha =2$?? $\sin \alpha \in [-1;1]$ với mọi $\alpha$ mà bạn. Bạn xem lại đề.

a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)

Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2

\(1+tan^2a=\dfrac{1}{cos^2a}=1:\dfrac{1}{25}=25\)
=>tan^2a=24
=>tana=2*căn 6
\(cota=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)
\(sina=\sqrt{1-\left(\dfrac{1}{5}\right)^2}=\dfrac{2\sqrt{6}}{5}\)

Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
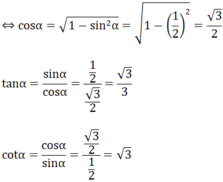

dung may tinh la xong thui ban oi
hoac dua len mang giai
chao <>?
Ta có:
\(cot\alpha\cdot tan\alpha=1\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}\)
\(\Rightarrow cota=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Mà:
\(cot^2\alpha+1=\dfrac{1}{sin^2\alpha}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{cot^2\alpha+1}}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{\left(\dfrac{4}{3}\right)^2+1}}=\dfrac{3}{5}\)
Lại có:
\(cos^2\alpha+sin^2\alpha=1\)
\(\Rightarrow cos\alpha=\sqrt{1-sin^2a}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
\(tan\alpha=\dfrac{3}{4}\\ \Rightarrow cot\alpha=1:\dfrac{3}{4}=\dfrac{4}{3}\)
Có:
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\\ \Rightarrow sin\alpha=\sqrt{1:\left(1+\left(\dfrac{4}{3}\right)^2\right)}=\dfrac{3}{5}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)