mng làm nhanh giúp mik nha.Làm bao nhiêu bào cx đc ah(lm hết càng tốt nhé).Cảm ơn mng gất nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 10 2021
ta có Cu ko tác dụng được vs H2SO4
-> 2,24 lít khí H2 đc tạo ra là do phản ứng HH của Fe va H2SO4
\(PTHH:\) \(Fe+H_2SO_4->FeSO_4+H2\)
n H2 = 2,24 :22,4=0,1 mol
n H2 = n Fe =0,1 mol
m Fe = 0,1.56=5,6 g
m Cu = 10-5,6=4,4 g
vậy giá trị của x là 4,4 g
3 tháng 10 2021
26
PTHH : \(Zn+2HCl->ZnCl_2+H_2\)
n Zn = 6,5:65=0,1 mol
n ZnCl2 = n Zn =0,1 mol
m ZnCl2 = 0,1.(65+35,5.2)=13,6 g
DM
5
KV
18 tháng 8 2023
Bài 2
a) x/8 = 5,4/3
x = 8 . 5,4/3
x = 14,4
b) 2,5 : 7,5 = x : 3/5
x = 3/5 × 1/3
x = 1/5
c) 2 2/3 : x = 1 7/9 : 0,2
8/3 : x = 16/9 : 1/5
x = 8/3 : (16/9 : 1/5)
x = 8/3 : 80/9
x = 3/10
d) 4/x = x/0,16
x² = 4 . 0,16
x² = 0,64
x = 0,8 hoặc x = -0,8
KV
18 tháng 8 2023
Bài 3
a) x/9 = y/11 và x + y = 60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/9 + y/11 = (x + y)/(9 + 11) = 60/20 = 3
x/9 = 3 ⇒ x = 9.3 = 27
y/11 = 3 ⇒ y = 11.3 = 33
Vậy x = 27; y = 33
b) x/3 = y/5 ⇒ 2x/6 = y/5 và 2x - y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/6 = y/5 = (2x - y)/(6 - 5) = 8/1 = 8
2x/6 = 8 ⇒ x = 6.8:2 = 24
y/5 = 8 ⇒ y = 5.8 = 40
Vậy x = 24; y = 40
c) 7x = 4y ⇒ y/7 = x/4 và y - x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
y/7 = x/4 = (y - x)/(7 - 4) = 24/3 = 8
x/4 = 8 ⇒ x = 4.8 = 32
y/7 = 8 ⇒ y = 7.8 = 56
Vậy x = 32; y = 56
NT
0
NV
3
AH
Akai Haruma
Giáo viên
11 tháng 8 2021
Bài 4:
a. ĐKXĐ: \(\left\{\begin{matrix} x-1\geq 0\\ x-1\neq 2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x\neq 3\end{matrix}\right.\)
b. \(B=\frac{x-3}{\frac{x-1-2}{\sqrt{x-1}+\sqrt{2}}}=\sqrt{x-1}+\sqrt{2}\)
\(x=4(2-\sqrt{3})\Rightarrow x-1=7-4\sqrt{3}=(2-\sqrt{3})^2\)
\(\Rightarrow \sqrt{x-1}=2-\sqrt{3}\Rightarrow B=\sqrt{x-1}+\sqrt{2}=2-\sqrt{3}+\sqrt{2}\)
c.
$\sqrt{x-1}\geq 0$ với mọi $x\geq 1; x\neq 3$
$\Rightarrow B=\sqrt{x-1}+\sqrt{2}\geq \sqrt{2}$
Vậy $B_{\min}=\sqrt{2}$ khi $x=1$
AH
Akai Haruma
Giáo viên
11 tháng 8 2021
Bài 5:
\(C=\frac{x-2\sqrt{xy}+y+4\sqrt{xy}}{\sqrt{x}+\sqrt{y}}-\frac{\sqrt{xy}(\sqrt{x}-\sqrt{y})}{\sqrt{xy}}\)
\(=\frac{(\sqrt{x}+\sqrt{y})^2}{\sqrt{x}+\sqrt{y}}-(\sqrt{x}-\sqrt{y})=(\sqrt{x}+\sqrt{y})-(\sqrt{x}-\sqrt{y})\)
\(=2\sqrt{y}\) vẫn phụ thuộc vào biến $y$ bạn ạ. Bạn xem lại đề.
NA
22 tháng 11 2021
Um có nhiều web học tiếng anh lắm ạ . Ví dụ như Langking dom hoặc Tieka . Tieka chỉ cần đóng 1 -> 2 triệu là có thể học từ giờ đến lớp 12 luôn ấy ạ . Có đủ bài giảng với có bài thực hành
2 tháng 7 2021
Câu 63: A
Câu 64: B
Câu 65: C
Câu 71: D
Câu 72: A
Câu 73: C
Câu 74: B
Câu 75: C
Câu 76: B
Câu 77: A
Câu 78: C
Câu 79: B
Câu 80: C
NC
1
27 tháng 9 2021
\(a,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{21}=\dfrac{5x}{50}=\dfrac{2z}{42}=\dfrac{5x+y-2z}{50+6-42}=\dfrac{28}{14}=2\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=12\\z=42\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x}{15}=\dfrac{y}{20};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{y}{20}=\dfrac{z}{28}\\ \Rightarrow\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}\)
Áp dụng t/c dtsbn
\(\dfrac{x}{15}=\dfrac{y}{20}=\dfrac{z}{28}=\dfrac{2x}{30}=\dfrac{3y}{60}=\dfrac{2x+3y-z}{30+60-28}=\dfrac{124}{62}=2\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=40\\z=56\end{matrix}\right.\)
\(c,\) Áp dụng t/c dtsbn
\(\dfrac{2x}{3}=\dfrac{3y}{4}=\dfrac{4z}{5}=\dfrac{x}{\dfrac{3}{2}}=\dfrac{y}{\dfrac{4}{3}}=\dfrac{z}{\dfrac{5}{4}}=\dfrac{x+y+z}{\dfrac{3}{2}+\dfrac{4}{3}+\dfrac{5}{4}}=\dfrac{49}{\dfrac{49}{12}}=12\\ \Rightarrow\left\{{}\begin{matrix}x=12\cdot\dfrac{3}{2}=18\\y=12\cdot\dfrac{4}{3}=16\\z=12\cdot\dfrac{5}{4}=15\end{matrix}\right.\)
\(d,\) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Rightarrow x=2k;y=3k\)
\(xy=54\Rightarrow2k\cdot3k=54\Rightarrow k^2=9\Rightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=6;y=9\\x=-6;y=-9\end{matrix}\right.\)
\(e,\) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\Rightarrow x=5k;y=3k\)
\(x^2-y^2=4\Rightarrow25k^2-9k^2=4\Rightarrow16k^2=4\Rightarrow k^2=\dfrac{1}{4}\\ \Rightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2};y=\dfrac{3}{2}\\x=-\dfrac{5}{2};y=-\dfrac{3}{2}\end{matrix}\right.\)
\(f,\) Áp dụng t/c dtsbn:
\(\dfrac{x}{y+z+1}=\dfrac{y}{z+x+1}=\dfrac{z}{x+y-2}=\dfrac{x+y+z}{2\left(x+y+z\right)}=\dfrac{1}{2}=x+y+z\)
\(\Rightarrow\left\{{}\begin{matrix}2x=y+z+1\\2y=x+z+1\\2z=x+y-2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x+y+z=3x-1\\x+y+z=3y-1\\x+y+z=3z+2\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}3x-1=\dfrac{1}{2}\\3y-1=\dfrac{1}{2}\\3z+2=\dfrac{1}{2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{2}\\z=-\dfrac{1}{2}\end{matrix}\right.\)
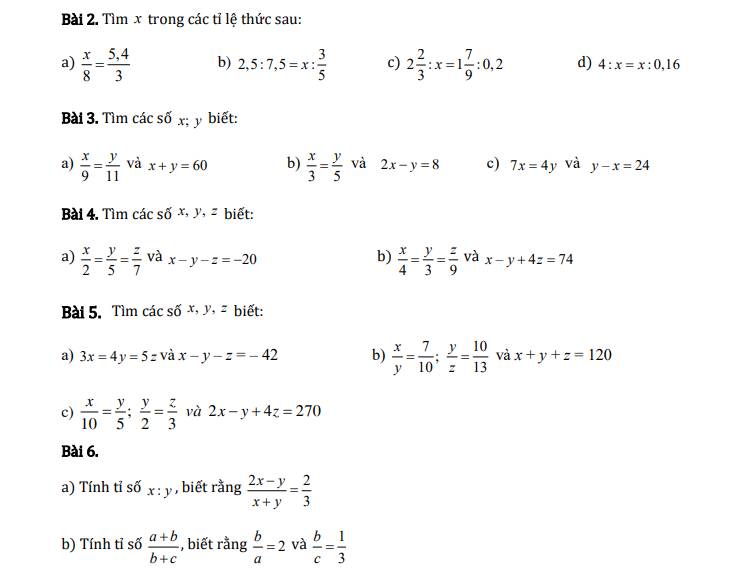
Bài 1:
a. $\frac{x}{2}=\frac{3,6}{1,2}=3$
$x=3.2=6$
b.
$\frac{8}{2x+1}=\frac{4}{3}$
$2x+1=\frac{8.3}{4}=6$
$2x=6-1=5$
$x=\frac{5}{2}$
c. $\frac{x}{4}=\frac{9}{x}$
$x^2=9.4=36=6^2=(-6)^2$
$\Rightarrow x=\pm 6$
d.
$\frac{x+1}{2}=\frac{32}{x+1}$
$(x+1)^2=32.2=64=8^2=(-8)^2$
$\Rightarrow x+1=8$ hoặc $x+1=-8$
$\Rightarrow x=7$ hoặc $x=-9$