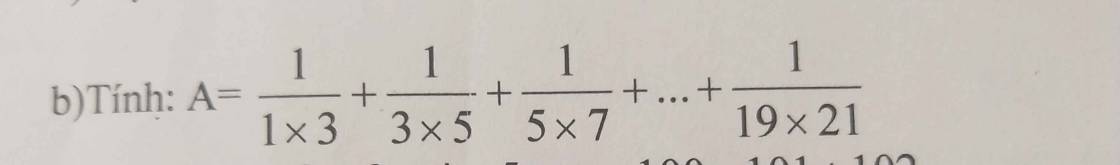ai giải giúp tớ với ạ! Tớ cảm ơn <3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
1
Những câu hỏi liên quan
TL
0
DN
1
HP
20 tháng 11 2021
a) (P) có đỉnh I(-1; -2)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{\Delta}{4a}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2.2\\b^2-4.2.c=8.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-8c=16\end{matrix}\right.\Leftrightarrow4^2-8c=16\)
\(\Leftrightarrow c=0\)
=> y = 2x2 + 4x
b) (P) có trục đối xứng x = 1 và cắt trục tung tại M(0; 4)
\(M\in\left(P\right)\Rightarrow4=2.0^2+b.0+c\)
\(\Leftrightarrow c=4\)
Trục đối xứng: \(x=-\dfrac{b}{2a}=1\)
<=> -b = 2a
<=> -b = 2.2
<=> b = -4
=> y = 2x2 - 4x + 4
c) Đi qua 2 điểm A(1; 6), B(-1; 0)
\(A\in\left(P\right)\Rightarrow6=2.1^2+b.1+c\)
\(\Leftrightarrow b+c=4\) (1)
\(B\in\left(P\right)\Rightarrow0=2.\left(-1\right)^2+b\left(-1\right)+c\)
\(\Leftrightarrow-b+c=-2\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}b+c=4\\-b+c=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\c=1\end{matrix}\right.\)
=> y = 2x2 + 3x + 1
TL
0
AT
16 tháng 7 2021
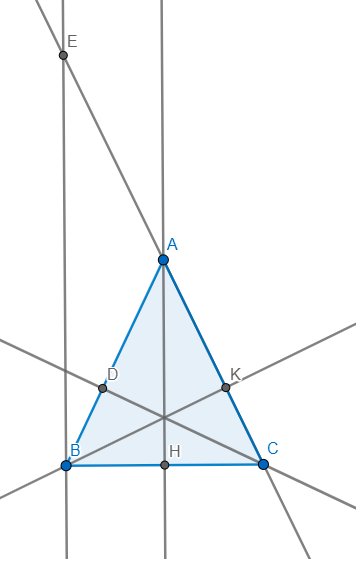
b) Từ B kẻ đường vuông góc với BC cắt AC tại E
tam giác BEC vuông tại B có \(AB=AC\Rightarrow A\) là trung điểm CE
Vì tam giác ABC cân tại A có AH là đường cao \(\Rightarrow H\) là trung điểm BC
\(\Rightarrow AH\) là đường trung bình tam giác BEC
\(\Rightarrow AH=\dfrac{1}{2}BE\Rightarrow2AH=BE\Rightarrow4AH^2=BE^2\)
tam giác BEC vuông tại B có BK là đường cao \(\Rightarrow\dfrac{1}{BE^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
\(\Rightarrow\dfrac{1}{4AH^2}+\dfrac{1}{BC^2}=\dfrac{1}{BK^2}\)
TT
0
2 tháng 2 2022
- Xét △OBC có: \(BC\)//\(AD\) (gt).
=>\(\dfrac{OD}{OC}=\dfrac{OA}{OB}\) (định lí Ta-let).
=>\(OD=\dfrac{OA}{OB}.OC=\dfrac{2,5}{2}.3=3,75\) (cm).
18 tháng 3 2023
`861000 cm^3=0,861 m^3`
`6,5 dm^3=6500 cm^3`
`40 m^3= 40000dm^3`
`2/3 dm^3=400 cm^3`
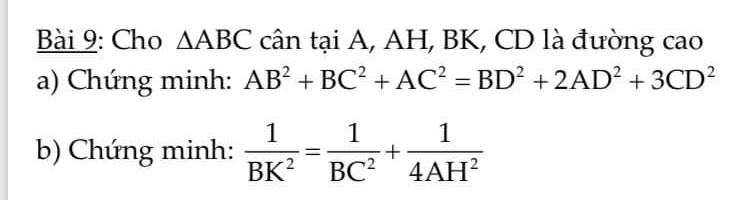
`#040911`
`b)`
\(A=\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{19\times21}\)
`=`\(\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{19\times21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\)
`=`\(\dfrac{1}{2}\times\left(1-\dfrac{1}{21}\right)\)
\(=\dfrac{1}{2}\times\dfrac{20}{21}\\ =\dfrac{10}{21}\\ \text{ Vậy, A = }\dfrac{10}{21}\)