Hãy 2 dựng tiếp tuyến chung ngoài của 2 đường tròn bằng thước và compa.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


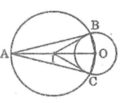
* Phân tích
Giả sử tiếp tuyến AB và AC cần dựng thỏa mãn điều kiện bài toán
Ta có: AB ⊥ OB ⇒ ∠ ABO = 90 °
AC ⊥ OC ⇒ ∠ ACO = 90 °
Tam giác ABO có ∠ ABO = 90 ° nội tiếp trong đường tròn đường kính AO và tam giác ACO có ∠ ACO = 90o nội tiếp trong đường tròn đường kính AO.
Suy ra B và C là giao điểm của đường tròn đường kính AO với đường tròn (O).
* Cách dựng
- Dựng I là trung điểm của OA
- Dựng đường tròn (I; IO) cắt đường tròn (O) tại B và C
- Nối AB, AC ta được hai tiếp tuyến cần dựng
* Chứng minh
Tam giác ABO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ABO = 90 °
Suy ra: AB ⊥ OB tại B nên AB là tiếp tuyến của đường tròn (O)
Tam giác ACO nội tiếp trong đường tròn (I) có OA là đường kính nên: ∠ ACO = 90 °
Suy ra: AC ⊥ OC tại C nên AC là tiếp tuyến của đường tròn (O)
* Biện luận
Luôn dựng được đường tròn tâm I, cắt đường tròn tâm O tại hai điểm B và C và luôn có AB, AC là hai tiếp tuyến của đường tròn (O).


AB vuông góc OB tại B nên AB là tiếp tuyến của đường tròn (O). Tương tự, AC là tiếp tuyến của đường tròn (O)

Bạn lấy điểm E là trung điểm của OA, xong vẽ đường tròn bán kính AE cắt (O) tại B,C; nối hai đường AB,AC, ta được AB,AC là các tiếp tuyến cần vẽ

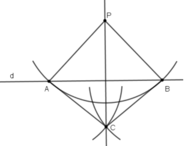
a) Ta có: PA = PB (A; B nằm trên cung tròn tâm P) nên P nằm trên đường trung trực của AB.
CA = CB (C nằm trên 2 cung tròn tâm A, B bán kính bằng nhau) nên C nằm trên đường trung trực của AB.
Vậy CP là đường trung trực của AB, suy ra PC ⊥ d.
b) Một cách vẽ khác
- Lấy hai điểm A, B bất kì trên d.
- Vẽ cung tròn tâm A bán kính AP, cung tròn tâm B bán kính BP. Hai cung tròn cắt nhau tại C (C khác P).
- Vẽ đường thẳng PC. Khi đó PC là đường đi qua P và vuông góc với d.
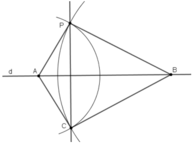
Chứng minh :
- Theo định lí 2 :
PA = CA ( P,C cùng thuộc cung tròn tâm A bán kính PA)
⇒ A thuộc đường trung trực của PC.
PB = CB (P, C cùng thuộc cung tròn tâm B bán kính PB)
⇒ B thuộc đường trung trực của PC.
⇒ AB là đường trung trực của PC
⇒ PC ⏊ AB hay PC ⏊ d.

a: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: IO là phân giác của góc DIA
=>\(\widehat{DIA}=2\cdot\widehat{OIA}\)
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IO' là phân giác của góc AIE
=>\(\widehat{AIE}=2\cdot\widehat{AIO'}\)
Ta có: \(\widehat{DIA}+\widehat{EIA}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{OIA}+\widehat{O'IA}\right)=180^0\)
=>\(2\cdot\widehat{OIO'}=180^0\)
=>\(\widehat{OIO'}=90^0\)
b: Xét (O) có
ID,IA là các tiếp tuyến
Do đó: ID=IA
Xét (O') có
IA,IE là các tiếp tuyến
Do đó: IA=IE
Ta có: IA=IE
ID=IA
Do đó: ID=IE
=>I là trung điểm của DE
=>I là tâm đường tròn đường kính DE
Xét ΔDAE có
AI là bán kính
\(AI=\dfrac{DE}{2}\)
Do đó: ΔADE vuông tại A
=>A nằm trên (I)
Xét (I) có
IA là bán kính
O'O\(\perp\)IA tại A
Do đó: OO' là tiếp tuyến của (I)
=>O'O là tiếp tuyến của đường tròn đường kính DE
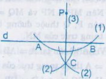
Giả sử ta cần dựng 2 tiếp tuyến chung ngoài AB,CD của (O;R) và (O';R') và R<R'.
C1: Lấy điểm E bất kì trên (O). Dựng đường thẳng qua O' song song với OE và cắt (O') tại F (E,F nằm cùng phía so với OO').
EF cắt OO' tại I. Dùng com-pa để vẽ hai đường tròn có đường kính lần lượt là OI và O'I, cắt (O) tại A,C và cắt (O') tại B,D.
=>AB,CD là 2 tiếp tuyến chung ngoài của (O) và (O').
C2: Vẽ đường tròn đường kính OO' và đường tròn (O';R'-R), hai đường tròn đó cắt nhau tại I. O'I kéo dài cắt (O') tại 2 điểm B,D. Dựng đường thẳng song song với O'I cắt (O) tại 2 điểm A,C.
=>.....
=))))))))))))))))))))