tim x^2023+y^2024+z^2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
2
YN
9 tháng 2 2023
\(x+\left(x+1\right)+\left(x+2\right)+...+2023+2024=2024\)
\(\Rightarrow2023x+4090506=2024-2024-20232023\)
\(\Rightarrow x+4090506=-2023\)
\(\Rightarrow2023x=-2023-4090506\)
\(\Rightarrow2023x=-4092529\)
\(\Rightarrow x=-2023\).
AH
Akai Haruma
Giáo viên
15 tháng 7 2023
Lời giải:
Ta có:
$(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})=2023.\frac{2024}{2023}$
$\Leftrightarrow 1+\frac{x}{y}+\frac{x}{z}+\frac{y}{x}+1+\frac{y}{z}+\frac{z}{x}+\frac{z}{y}+1=2024$
$\Leftrightarrow 3+\frac{x+z}{y}+\frac{y+z}{x}+\frac{x+y}{z}=2024$
$\Leftrightarrow 3+B=2024$
$\Leftrightarrow B=2021$
25 tháng 12 2023
a: \(\left|a-2b+3\right|^{2023}>=0\forall a,b\)
\(\left(b-1\right)^{2024}>=0\forall b\)
Do đó: \(\left|a-2b+3\right|^{2023}+\left(b-1\right)^{2024}>=0\forall a,b\)
Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}a-2b+3=0\\b-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=1\\a=2b-3=2\cdot1-3=-1\end{matrix}\right.\)
Thay a=-1 và b=1 vào P, ta được:
\(P=\left(-1\right)^{2023}\cdot1^{2024}+2024=2024-1=2023\)
2 tháng 9
a: Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|y-2\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|y-2\right|\ge0\forall x,y\)
=>\(-\left|x+2\right|-\left|y-2\right|\le0\forall x,y\)
=>\(A=-\left|x+2\right|-\left|y-2\right|+2024\le2024\forall x,y\)
Dấu '=' xảy ra khi \(\begin{cases}x+2=0\\ y-2=0\end{cases}\Rightarrow\begin{cases}x=-2\\ y=2\end{cases}\)
b: Ta có: \(\left|2x+5\right|\ge0\forall x\)
=>\(\left|2x+5\right|+2024\ge2024\forall x\)
=>\(B=\frac{2023}{\left|2x+5\right|+2024}\le\frac{2023}{2024}\forall x\)
Dấu '=' xảy ra khi 2x+5=0
=>2x=-5
=>\(x=-\frac52\)
TH
Trần Hoàng Trung
VIP
2 tháng 9
a) Tìm giá trị lớn nhất của \(A = 2024 - \mid x + 2 \mid - \mid y - 2 \mid\)
Biểu thức \(A\) có chứa các giá trị tuyệt đối \(\mid x + 2 \mid\) và \(\mid y - 2 \mid\). Để \(A\) có giá trị lớn nhất, chúng ta cần làm sao cho các giá trị tuyệt đối này nhỏ nhất, bởi vì \(A\) là một hiệu và giá trị tuyệt đối luôn không âm. Do đó, \(A\) sẽ lớn nhất khi các biểu thức trong giá trị tuyệt đối đạt giá trị bằng 0.
Phân tích chi tiết:
- \(\mid x + 2 \mid\) đạt giá trị nhỏ nhất bằng 0 khi \(x = - 2\).
- \(\mid y - 2 \mid\) đạt giá trị nhỏ nhất bằng 0 khi \(y = 2\).
Vậy, khi \(x = - 2\) và \(y = 2\), ta có:
\(A = 2024 - \mid x + 2 \mid - \mid y - 2 \mid = 2024 - 0 - 0 = 2024\)
Do đó, giá trị lớn nhất của \(A\) là 2024.
b) Tìm giá trị lớn nhất của \(B = \frac{2023}{\mid 2 x + 5 \mid} + 2024\)
Biểu thức \(B\) có dạng tổng của hai phần, trong đó phần thứ nhất là \(\frac{2023}{\mid 2 x + 5 \mid}\) và phần thứ hai là một hằng số \(2024\). Để tìm giá trị lớn nhất của \(B\), chúng ta cần làm sao cho phần \(\frac{2023}{\mid 2 x + 5 \mid}\) đạt giá trị lớn nhất.
Phân tích chi tiết:
- Phần \(\frac{2023}{\mid 2 x + 5 \mid}\) có giá trị lớn nhất khi \(\mid 2 x + 5 \mid\) nhỏ nhất. Vì \(\mid 2 x + 5 \mid \geq 0\), ta cần \(\mid 2 x + 5 \mid\) càng nhỏ càng tốt.
- \(\mid 2 x + 5 \mid\) đạt giá trị nhỏ nhất bằng 0 khi \(2 x + 5 = 0\), tức là \(x = - \frac{5}{2}\).
Vậy khi \(x = - \frac{5}{2}\), ta có:
\(B = \frac{2023}{\mid 2 x + 5 \mid} + 2024 = \frac{2023}{0} + 2024\)
Tuy nhiên, chia cho 0 là không xác định và không thể đạt được giá trị tại \(x = - \frac{5}{2}\). Vì vậy, ta không thể chọn \(x = - \frac{5}{2}\).
Tuy nhiên, khi \(\mid 2 x + 5 \mid\) càng lớn, phần \(\frac{2023}{\mid 2 x + 5 \mid}\) sẽ càng nhỏ, và ta muốn giá trị của \(\frac{2023}{\mid 2 x + 5 \mid}\) càng nhỏ thì \(B\) sẽ đạt giá trị tối thiểu. Giá trị lớn nhất của \(B\) sẽ đạt được khi \(\mid 2 x + 5 \mid\) đạt giá trị nhỏ nhất nhưng không bằng 0.
Do đó, giá trị lớn nhất có thể đạt được cho \(B\) khi \(2 x + 5\) càng gần 0.
30 tháng 8
Ta có: x+y+z=0
=>\(\left(x+y+z\right)^2=0^2=0\)
=>\(x^2+y^2+z^2+2\left(xy+yz+xz\right)=0\)
=>\(x^2+y^2+z^2=0\)
mà \(x^2\ge0\forall x;y^2\ge0\forall y;z^2\ge0\forall z\)
nên \(\begin{cases}x=0\\ y=0\\ z=0\end{cases}\)
\(\left(x-1\right)^{2023}+y^{2024}+\left(z+1\right)^{2025}\)
\(=\left(0-1\right)^{2023}+0^{2024}+\left(0+1\right)^{2025}\)
=-1+0+1
=0
30 tháng 8
Ta có: x+y+z=0
=>\(\left(x+y+z\right)^2=0^2=0\)
=>\(x^2+y^2+z^2+2\left(xy+yz+xz\right)=0\)
=>\(x^2+y^2+z^2=0\)
mà \(x^2\ge0\forall x;y^2\ge0\forall y;z^2\ge0\forall z\)
nên \(\begin{cases}x=0\\ y=0\\ z=0\end{cases}\)
\(\left(x-1\right)^{2023}+y^{2024}+\left(z+1\right)^{2025}\)
\(=\left(0-1\right)^{2023}+0^{2024}+\left(0+1\right)^{2025}\)
=-1+0+1
=0
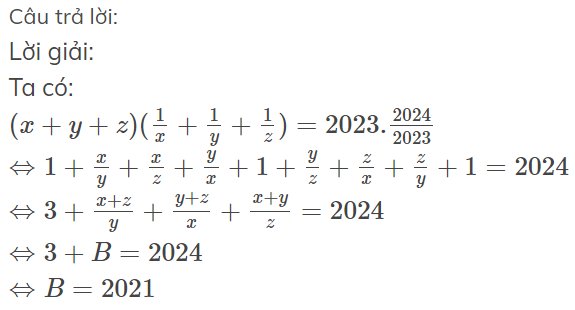
Đề không đầy đủ. Bạn coi lại.