còn nè
trong khoảng từ 1;2;3;4;..........2017Có tất cả bao nhiêu số
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
27 tháng 3 2021
\(\Delta:2x+y-1=0\)
Gọi \(C=\left(0;m\right)\) thuộc trục tung.
Ta có \(d\left(C;\Delta\right)=3d\left(B;\Delta\right)\)
\(\Leftrightarrow\dfrac{5\left|2.1+2.1-1\right|}{\sqrt{2^2+1^2}}=\dfrac{\left|2.0+1.m-1\right|}{\sqrt{2^2+1^2}}\)
\(\Leftrightarrow\left|m+1\right|=15\)
\(\Leftrightarrow\left[{}\begin{matrix}m=14\\m=-16\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}C=\left(0;14\right)\left(\text{loại do cùng phía với }\Delta\right)\\C=\left(0;-16\right)\end{matrix}\right.\)
\(\Rightarrow C=\left(0;-16\right)\)
Lấy B' đối xứng với B qua \(\Delta\), M là giao điểm của BB' và \(\Delta\)
BB' có phương trình: \(x-2y+3=0\)
M có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}2x+y-1=0\\x-2y+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=\dfrac{7}{5}\end{matrix}\right.\Rightarrow M=\left(-\dfrac{1}{5};\dfrac{7}{5}\right)\)
\(\Rightarrow B'=\left(-\dfrac{7}{5};\dfrac{4}{5}\right)\)
AC có phương trình \(\dfrac{x}{0+\dfrac{7}{5}}=\dfrac{y+16}{-16-\dfrac{4}{5}}\Leftrightarrow84x+7y+112=0\)
A có tọa độ là nghiệm hệ \(\left\{{}\begin{matrix}84x+7y+112=0\\2x+y-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{17}{10}\\y=\dfrac{22}{5}\end{matrix}\right.\Rightarrow A\left(-\dfrac{17}{10};\dfrac{22}{5}\right)\)
VT
24 tháng 8 2018
Đáp án C
Phương pháp:
-Sử dụng lí thuyết về dao động điện từ
- Sử dung̣ vòng tròn lương̣ giác
Cách giải:
- Khoảng thời gian để cường độ dòng điện qua cuộn cảm giảm từ độ lớn cực đại xuống còn một nửa độ lớn cực đại là:
 |
-
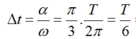
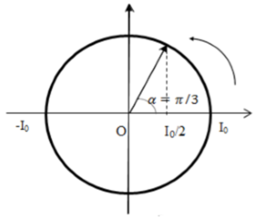
- Năng lượng từ trường trong mạch cực đại: i = ± I0
- Năng lượng tư trường bằng nửa giá trị cực đại:
 |
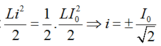
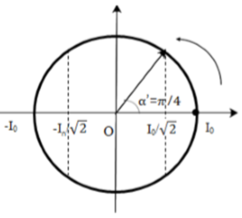=> Khoảng thời gian ngắn nhất để năng lượng từ trường trong mạch giảm từ độ lớn cực đại xuống còn một nửa giá trị đó là:
VT
15 tháng 3 2018
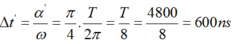
- Khoảng thời gian ngắn nhất để dòng điện giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là:
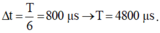
- Năng lượng từ trường trong mạch giảm từ cực đại đến còn một nửa trong khoảng thời gian:
VT
19 tháng 1 2017
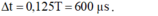
Khoảng thời gian ngắn nhất để dòng điện giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là ∆t = T/6 = 800μs→ T = 4800 μs.
+ Năng lượng từ trường trong mạch giảm từ cực đại đến còn một nửa trong khoảng thời gian ∆t = 0,125T = 600 μs.
Chọn đáp án C
VT
3 tháng 11 2018
+ Khoảng thời gian ngắn nhất để dòng điện giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là .
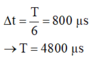
+ Năng lượng từ trường trong mạch giảm từ cực đại đến còn một nửa trong khoảng thời gian
.
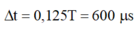Đáp án C
VT
31 tháng 1 2019
Đáp án C
+ Khoảng thời gian ngắn nhất để dòng điện giảm từ giá trị cực đại xuống còn một nửa giá trị cực đại là Δ t = T 6 = 800 μ s → T = 4800 μ s
+ Năng lượng từ trường trong mạch giảm từ cực đại đến còn một nửa trong khoảng thời gian Δ t = 0 , 125 T = 600 μ s
có 2017 số nha bạn
có tất cả số là(2017-1):1+1=2017